
【题目】现有甲,乙两种不透明充气包装的袋装零食,每袋零食甲随机附赠玩具![]() ,
,![]() ,
,![]() 中的一个,每袋零食乙从玩具
中的一个,每袋零食乙从玩具![]() ,
,![]() 中随机附赠一个.记事件
中随机附赠一个.记事件![]() :一次性购买
:一次性购买![]() 袋零食甲后集齐玩具
袋零食甲后集齐玩具![]() ,
,![]() ,
,![]() ;事件
;事件![]() :一次性购买
:一次性购买![]() 袋零食乙后集齐玩具
袋零食乙后集齐玩具![]() ,
,![]() .
.
(1)求概率![]() ,
,![]() 及
及![]() ;
;
(2)已知![]() ,其中
,其中![]() ,
,![]() 为常数,求
为常数,求![]() .
.
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)
;(2)![]()
【解析】
(1)一次性购买4袋零食甲获得玩具的情况共有![]() 种不同的可能,其中能够集齐三种玩具的充要条件是
种不同的可能,其中能够集齐三种玩具的充要条件是![]() ,
,![]() ,
,![]() 三个玩具中,某个玩具出现两次,其余玩具各出现一次, 计算得到概率,同理可得答案.
三个玩具中,某个玩具出现两次,其余玩具各出现一次, 计算得到概率,同理可得答案.
(2)记![]() ,
,![]() ,计算
,计算![]() ,得到
,得到![]() ,利用累加法计算得到答案.
,利用累加法计算得到答案.
(1)一次性购买4袋零食甲获得玩具的情况共有![]() 种不同的可能,
种不同的可能,
其中能够集齐三种玩具的充要条件是![]() ,
,![]() ,
,![]() 三个玩具中,某个玩具出现两次,其余玩具各出现一次,对应的可能性为
三个玩具中,某个玩具出现两次,其余玩具各出现一次,对应的可能性为![]() ,故
,故![]() ,
,
一次性购买5袋零食甲获得玩具的情况共有![]() 不同的可能,
不同的可能,
其中能够集齐三种玩具的充要条件是![]() ,
,![]() ,
,![]() 三个玩具中,某个玩具出现三次,其余玩具各出现一次或某两个玩具各出现两次,另一个玩具出现一次,对应的可能性分别为
三个玩具中,某个玩具出现三次,其余玩具各出现一次或某两个玩具各出现两次,另一个玩具出现一次,对应的可能性分别为![]() ,
,![]() ,
,
故![]() .
.
一次性购买4袋零食乙获得玩具的情况共有![]() 种不同的可能,
种不同的可能,
其中不能集齐两种玩具的情况只有2种,即全是![]() ,全是
,全是![]() ,故
,故![]() .
.
(2)记![]() ,
,![]() ,根据题意及(1)的计算,不难整理得下表:
,根据题意及(1)的计算,不难整理得下表:
| 1 | 2 | 3 | 4 | 5 |
| 0 | 0 |
|
|
|
| 0 |
|
|
| … |
由于![]() 的对立事件总是2种情形(即全是
的对立事件总是2种情形(即全是![]() ,全是
,全是![]() ),
),
容易得到![]() .
.
为解出待定系数![]() ,
,![]() ,令
,令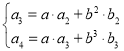 ,即
,即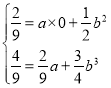 ,
,
解得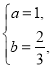 或
或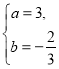 (舍去,因为
(舍去,因为![]() ).
).
故![]() ,即
,即![]() ,
,
同理![]() ,
,
……
![]() ,
,
累加可得![]() (
(![]() ).
).
当![]() 时,
时,![]() 适合上式,∴
适合上式,∴![]() .
.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:
【题目】已知F(0,1)为平面上一点,H为直线l:y=﹣1上任意一点,过点H作直线l的垂线m,设线段FH的中垂线与直线m交于点P,记点P的轨迹为Γ.
(1)求轨迹Γ的方程;
(2)过点F作互相垂直的直线AB与CD,其中直线AB与轨迹Γ交于点AB,直线CD与轨迹Γ交于点CD,设点M,N分别是AB和CD的中点.
①问直线MN是否恒过定点,如果经过定点,求出该定点,否则说明理由;
②求△FMN的面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 与直线
与直线![]() 相切于点
相切于点![]() ,点
,点![]() 与
与![]() 关于
关于![]() 轴对称.
轴对称.
(1)求抛物线![]() 的方程及点
的方程及点![]() 的坐标;
的坐标;
(2)设![]() 是
是![]() 轴上两个不同的动点,且满足
轴上两个不同的动点,且满足![]() ,直线
,直线![]() 、
、![]() 与抛物线
与抛物线![]() 的另一个交点分别为
的另一个交点分别为![]() ,试判断直线
,试判断直线![]() 与直线
与直线![]() 的位置关系,并说明理由.如果相交,求出的交点的坐标.
的位置关系,并说明理由.如果相交,求出的交点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国际上通常用年龄中位数指标作为划分国家或地区人口年龄构成的标准:年龄中位数在20岁以下为“年轻型”人口;年龄中位数在20~30岁为“成年型”人口;年龄中位数在30岁以上为“老龄型”人口.

如图反映了我国全面放开二孩政策对我国人口年龄中位数的影响.据此,对我国人口年龄构成的类型做出如下判断:①建国以来直至2000年为“成年型”人口;②从2010年至2020年为“老龄型”人口;③放开二孩政策之后我国仍为“老龄型”人口.其中正确的是( )
A.②③B.①③C.②D.①②
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() 过点
过点![]() ,离心率为
,离心率为![]() ,
,![]() 分别是椭圆
分别是椭圆![]() 的左、右顶点,过右焦点
的左、右顶点,过右焦点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点.
两点.
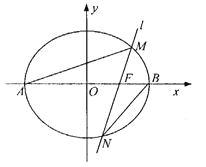
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)记![]() 、
、![]() 的面积分别为
的面积分别为![]() 、
、![]() ,若
,若![]() ,求
,求![]() 的值;
的值;
(3)记直线![]() 、
、![]() 的斜率分别为
的斜率分别为![]() 、
、![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为筛查在人群中传染的某种病毒,现有两种检测方法:
(1)抗体检测法:每个个体独立检测,每一次检测成本为80元,每个个体收取检测费为100元.
(2)核酸检测法:先合并个体,其操作方法是:当个体不超过10个时,把所有个体合并在一起进行检测.
当个体超过10个时,每10个个体为一组进行检测.若该组检测结果为阴性(正常),则只需检测一次;若该组检测结果为阳性(不正常),则需再对每个个体按核酸检测法重新独立检测,共需检测k+1次(k为该组个体数,1≤k≤10,k∈N*).每一次检测成本为160元.假设在接受检测的个体中,每个个体的检测结果是阳性还是阴性相互独立,且每个个体是阳性结果的概率均为p(0<p<1).
(Ⅰ)现有100个个体采取抗体检测法,求其中恰有一个检测出为阳性的概率;
(Ⅱ)因大多数人群筛查出现阳性的概率很低,且政府就核酸检测法给子检测机构一定的补贴,故检测机构推出组团选择核酸检测优惠政策如下:无论是检测一次还是k+1次,每组所有个体共收费700元(少于10个个体的组收费金额不变).已知某企业现有员工107人,准备进行全员检测,拟准备9000元检测费,由于时间和设备条件的限制,采用核酸检测法合并个体的组数不得高于参加采用抗体检测法人数,请设计一个合理的的检测安排方案;
(Ⅲ)设![]() ,现有n(n∈N*且2≤n≤10)个个体,若出于成本考虑,仅采用一种检测方法,试问检测机构应采用哪种检测方法?(ln3≈1.099,ln4≈1.386,ln5≈1.609,ln6≈1.792)
,现有n(n∈N*且2≤n≤10)个个体,若出于成本考虑,仅采用一种检测方法,试问检测机构应采用哪种检测方法?(ln3≈1.099,ln4≈1.386,ln5≈1.609,ln6≈1.792)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 为抛物线的焦点,
为抛物线的焦点,![]() 是过焦点的动弦,
是过焦点的动弦,![]() 是
是![]() 两点在准线上的投影,如图所示,则下列论断正确的个数有( )
两点在准线上的投影,如图所示,则下列论断正确的个数有( )
①以![]() 为直径的圆与准线一定相切;
为直径的圆与准线一定相切;
②以![]() 为直径的圆与直线
为直径的圆与直线![]() 一定相切;
一定相切;
③以![]() 为直径的圆与
为直径的圆与![]() 轴一定相切;
轴一定相切;
④以![]() 为直径的圆与
为直径的圆与![]() 轴有可能相切
轴有可能相切
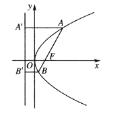
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com