
| A. | 199 | B. | 200 | C. | 99 | D. | 100 |
分析 求出椭圆的a,b,c,利用等差数列的通项公式和|PiF|的最大值和最小值分别为a+c,a-c,结合不等式的性质即可得出n的最大值.
解答 解:椭圆$\frac{x^2}{4}$+$\frac{y^2}{3}$=1的a=2,b=$\sqrt{3}$,c=1,
∵|P1F|,|P2F|,…,|PnF|组成等差数列,
∴|PnF|=|P1F|+(n-1)d.
∵|PnF|≤a+c,|P1F|≥a-c,
∴|PnF|-|P1F|≤(a+c)-(a-c)=2c=2,
又公差d>$\frac{1}{100}$,
∴n≤$\frac{2}{d}$+1<201,
∴n的最大值是200,
故选:B.
点评 本题考查椭圆的方程和性质,考查等差数列的通项公式的运用,运用椭圆上的点与焦点的距离的最值和不等式的性质是解题的关键.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
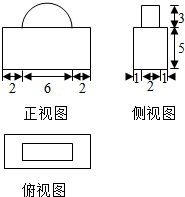 将一个长、宽、高分别为10、4、8的长方体毛坯加工成某工件,如图为加工后该工件的三视图,则该工件的材料利用率(材料利用率=$\frac{新工件的体积}{毛坯的体积}$)是$\frac{200+9π}{320}$.
将一个长、宽、高分别为10、4、8的长方体毛坯加工成某工件,如图为加工后该工件的三视图,则该工件的材料利用率(材料利用率=$\frac{新工件的体积}{毛坯的体积}$)是$\frac{200+9π}{320}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | log23 | B. | 2 | C. | log25 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
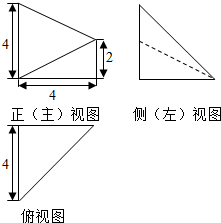
| A. | 4 | B. | 4$\sqrt{2}$ | C. | 4$\sqrt{3}$ | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
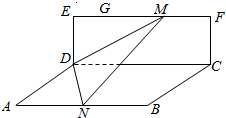 如图,矩形CDEF所在的平面与矩ABCD所在的平面垂直,AD=$\sqrt{2}$,DE=$\sqrt{3}$,AB=4,$\overrightarrow{EG}$=$\frac{1}{4}$$\overrightarrow{EF}$,点M在线段GF上(包括两端点),点N在线段AB上,且$\overrightarrow{GM}$=$\overrightarrow{AN}$,则二面角M-DN-B的平面角的取值范围为[$\frac{π}{4}$,$\frac{π}{3}$].
如图,矩形CDEF所在的平面与矩ABCD所在的平面垂直,AD=$\sqrt{2}$,DE=$\sqrt{3}$,AB=4,$\overrightarrow{EG}$=$\frac{1}{4}$$\overrightarrow{EF}$,点M在线段GF上(包括两端点),点N在线段AB上,且$\overrightarrow{GM}$=$\overrightarrow{AN}$,则二面角M-DN-B的平面角的取值范围为[$\frac{π}{4}$,$\frac{π}{3}$].查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
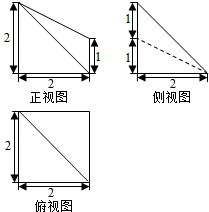
| A. | 8 | B. | $\frac{8}{3}$ | C. | $\frac{10}{3}$ | D. | $\frac{14}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com