
分析 (I)利用等比数列的通项公式即可得出;
(II)利用等差数列与等比数列的通项公式及其前n项和公式即可的.
解答 解:(Ⅰ)设等比数列{an}的首项为a1,公比为q.∵a3=4,a6=32.
∴$\left\{\begin{array}{l}{{a}_{1}{q}^{2}=4}\\{{a}_{1}{q}^{3}=32}\end{array}\right.$,解得a1=1,q=2.
∴an=2n-1.
(Ⅱ)设等差数列{bn}的首项为b1,公差为d.
∵b2=1,b4=a1+a3,
∴$\left\{\begin{array}{l}{{b}_{1}+d=1}\\{{b}_{1}+3d=1+4}\end{array}\right.$,解得d=2,b1=-1.
∴bn=-1+2(n-1)=2n-3.
∴an+bn=2n-1+(2n-3).
∴数列{an+bn}的前n项和Tn=$\frac{{2}^{n}-1}{2-1}$+$\frac{n(-1+2n-3)}{2}$=2n-1-2n+n2.
点评 本题考查了等差数列与等比数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 199 | B. | 200 | C. | 99 | D. | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 队员 | 1号 | 2号 | 3号 | 4号 | 5号 |
| A队 | 6 | 5 | 7 | 9 | 8 |
| B队 | 4 | 8 | 9 | 7 | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
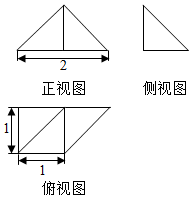 如图是一个几何体的三视图,正视图是一个等腰直角三角形,侧视图为一个直角三角形,俯视图是一个直角梯形,则此几何体的表面积是( )
如图是一个几何体的三视图,正视图是一个等腰直角三角形,侧视图为一个直角三角形,俯视图是一个直角梯形,则此几何体的表面积是( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{5+\sqrt{3}}{2}$ | D. | $\frac{5+\sqrt{3}}{2}$+$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
| 年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | |a|>|b| | B. | $\frac{b}{a}<1$ | C. | lga<lgb | D. | ${(\frac{1}{2})^a}<{(\frac{1}{2})^b}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com