
分析 (1)利用有理数指数幂性质、运算法则求解.
(2)利用对数性质、运算法则、换底公式求解.
解答 解:(1)${(5\frac{1}{16})^{0.5}}-2×{(2\frac{10}{27})^{-\frac{2}{3}}}-2×{(\sqrt{2+π})^0}÷{(\frac{3}{4})^{-2}}$
=$\sqrt{\frac{81}{16}}-2×{(\frac{64}{27})^{-\frac{2}{3}}}-2÷{(\frac{4}{3})^2}$
=$\frac{9}{4}-2×{(\frac{3}{4})^2}-2×{(\frac{3}{4})^2}$=0.…(6分)
(2)${9^{{{log}_3}2}}-4{log_4}3•{log_{27}}8+\frac{1}{3}{log_6}8-2{log_{{6^{-1}}}}\sqrt{3}$
=${3^{{{log}_3}4}}-2+{log_6}2+{log_6}3$
=4-2+log66
=2+1=3.…(12分)
点评 本题考查指数式、对数式化简求值,是基础题,解题时要认真审题,注意指数、对数性质、运算法则换底公式的合理运用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
| x | 2 | 3 | 5 | 6 |
| y | 7 | 8-a | 9+a | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∨q | B. | (¬p)∧(¬q) | C. | p∨(¬q) | D. | p∧q |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
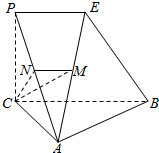 如图,在四棱锥A-BCPE中,侧面PAC为正三角形,∠ACB=90°,二面角P-AC-B为直二面角,PE∥BC且$\frac{PE}{CB}$=μ(μ>0),点M,N分别是侧棱AE、AP上的点,且$\frac{AM}{AE}$=$\frac{AN}{AP}$=λ(0<λ<1)
如图,在四棱锥A-BCPE中,侧面PAC为正三角形,∠ACB=90°,二面角P-AC-B为直二面角,PE∥BC且$\frac{PE}{CB}$=μ(μ>0),点M,N分别是侧棱AE、AP上的点,且$\frac{AM}{AE}$=$\frac{AN}{AP}$=λ(0<λ<1)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 199 | B. | 200 | C. | 99 | D. | 100 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com