
分析 设M$(\frac{{y}^{2}}{16},y)$,根据以MF为直径的圆过点A(0,2),可得$\overrightarrow{AM}•\overrightarrow{AF}$=0,解得y即可得出.
解答 解:F(4,0),
设M$(\frac{{y}^{2}}{16},y)$,∵以MF为直径的圆过点A(0,2),
∴AM⊥AF,
∴$\overrightarrow{AM}•\overrightarrow{AF}$=$(\frac{{y}^{2}}{16},y-2)$•(4,-2)=0,
∴$\frac{{y}^{2}}{4}-2(y-2)$=0,
解得y=4,
∴xM=$\frac{{4}^{2}}{16}$=1,
∴|MF|=1+4=5.
故答案为:5.
点评 本题考查了圆的性质、抛物线的定义及其性质、向量垂直与数量积的关系,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源:2017届云南曲靖市高三上半月考一数学试卷(解析版) 题型:选择题
在区间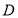 上,若函数
上,若函数 为增函数,而函数
为增函数,而函数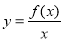 为减函数,则称函数
为减函数,则称函数 为区间
为区间 上的“弱增”函数.则下列函数中,在区间
上的“弱增”函数.则下列函数中,在区间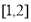 上不是“弱增”函数的为( )
上不是“弱增”函数的为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某企业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的体积为$\frac{80π}{3}$立方米,且l≥2r.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为c(c>5)千元.设该容器的建造费用为y千元.
某企业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的体积为$\frac{80π}{3}$立方米,且l≥2r.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为c(c>5)千元.设该容器的建造费用为y千元.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{27}$πa2 | B. | $\frac{32\sqrt{2}}{27}$πa2 | C. | $\frac{32\sqrt{3}}{27}$πa3 | D. | $\frac{32\sqrt{3}}{9}$πa3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | {x|x>1} | C. | {x|-1<x<0} | D. | {x|-1<x<0或x>1} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com