
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| ||
| 2 |
| 2 |
| a2 |
| 3 |
| 2b2 |
| 1 |
| 2 |
| x2 |
| 4 |
| y2 |
| 3 |
| y0 |
| 2 |
| y1 |
| x1-2 |
| 4y1 |
| x1+2 |
| y0y1 |
| 2(x1-2) |
| 4y12 | ||
2(
|
| y | 21 |
| 3 |
| 4 |
| x | 21 |
| 4y12 | ||
2(
|
| 3 |
| 2 |
| y1 |
| x1-2 |
| 2-x1 |
| y1 |
| 2-x1 |
| y1 |
| 2-x1 |
| y1 |
| 2-x1 |
| y1 |
| 2(2-x1) |
| y1 |
| 4y1 |
| x1+2 |
| 2-x1 |
| y1 |
2(x12-4)+4
| ||
| (x1+2)y1 |
| 2-x1 |
| y1 |
2(x12-4)+12-3
| ||
| (x1+2)y1 |
| 2-x1 |
| y1 |
| 2-x1 |
| y1 |
| 2-x1 |
| y1 |
| 2-x1 |
| y1 |



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃКВЛЯъ ЬтаЭЃКНтД№Ьт
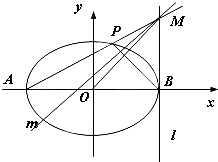
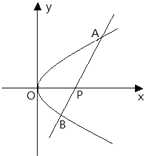
 ЃЌЦфНЙЕуFЃЈcЃЌ0ЃЉЃЈcЃО0ЃЉЖдгІЕФзМЯпlгыxжсНЛгкAЕуЃЌ|OF|=2|FA|ЃЌЙ§AЕФжБЯпгыЭждВНЛгкPЁЂQСНЕу.
ЃЌЦфНЙЕуFЃЈcЃЌ0ЃЉЃЈcЃО0ЃЉЖдгІЕФзМЯпlгыxжсНЛгкAЕуЃЌ|OF|=2|FA|ЃЌЙ§AЕФжБЯпгыЭждВНЛгкPЁЂQСНЕу.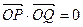 ЃЌЧѓжБЯпPQЕФЗНГЬЃЛ ЃЈ3ЃЉЩш
ЃЌЧѓжБЯпPQЕФЗНГЬЃЛ ЃЈ3ЃЉЩш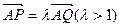 ЃЌЙ§ЕуPЧвЦНаагкзМЯпlЕФжБЯпгыЭждВЯрНЛгкСэвЛЕуM. ЧѓжЄFЁЂMЁЂQШ§ЕуЙВЯп.
ЃЌЙ§ЕуPЧвЦНаагкзМЯпlЕФжБЯпгыЭждВЯрНЛгкСэвЛЕуM. ЧѓжЄFЁЂMЁЂQШ§ЕуЙВЯп.ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃКВЛЯъ ЬтаЭЃКНтД№Ьт
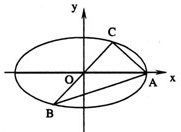
| AC |
| BC |
| PQ |
| AB |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃКВЛЯъ ЬтаЭЃКНтД№Ьт
| x2 |
| a2 |
| y2 |
| b2 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃКВЛЯъ ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃКВЛЯъ ЬтаЭЃКЬюПеЬт
| Іа |
| 3 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃКВЛЯъ ЬтаЭЃКНтД№Ьт
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| ||
| 2 |
| . |
| BM |
| . |
| BN |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃКВЛЯъ ЬтаЭЃКНтД№Ьт
| ||
| 3 |
| 6 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃКВЛЯъ ЬтаЭЃКНтД№Ьт
| 3 |
| 3 |
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com