
【题目】某城市先后采用甲、乙两种方案治理空气污染各一年,各自随机抽取一年(365天)内100天的空气质量指数API的检测数据进行分析,若空气质量指数值在[0,300]内为合格,否则为不合格.表1是甲方案检测数据样本的频数分布表,如图是乙方案检测数据样本的频率分布直方图.
表1:
API值 | [0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,300] | 大于300 |
天数 | 9 | 13 | 19 | 30 | 14 | 11 | 4 |
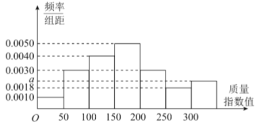
(1)将频率视为概率,求乙方案样本的频率分布直方图中![]() 的值,以及乙方案样本的空气质量不合格天数;
的值,以及乙方案样本的空气质量不合格天数;
(2)求乙方案样木的中位数;
(3)填写下面2×2列联表(如表2),并根据列联表判断是否有90%的把握认为该城市的空气质量指数值与两种方案的选择有关.
表2:
甲方案 | 乙方案 | 合计 | |
合格天数 | _______ | _______ | _______ |
不合格天数 | _______ | _______ | _______ |
合计 | _______ | _______ | _______ |
附: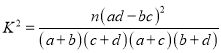
| 0.10 | 0.05 | 0.025 |
| 2.706 | 3.841 | 5.024 |
【答案】(1)![]() ,11天;(2)170;(3)表格见解析,有90%的把握认为该城市的空气质量指数值与两种方案的选择有关
,11天;(2)170;(3)表格见解析,有90%的把握认为该城市的空气质量指数值与两种方案的选择有关
【解析】
(1)根据频率和为1列出等式求解a,用乙方案样本中空气质量指数值大于300的频率乘以总天数即可得解;(2)根据中位数左边和右边的小长方形的面积和是相等的列出等式即可求得中位数;(3)由题意填写列联表,计算观测值,对照临界值得出结论.
(1)由频率分布直方图知,
![]() ,
,
解得![]() ,
,
∴乙方案样本中不合格天数为![]() (天);
(天);
(2)根据图1,得![]() ,
,
又![]() ,∵
,∵![]() ,
,
∴中位数在(150,200]之间,设中位数为![]() ,
,
则![]() ,解得
,解得![]() ,
,
∴乙方案样本的中位数为170;
(3)由题意填写![]() 列联表如下,
列联表如下,
甲方案 | 乙方案 | 合计 | |
合格天数 | 96 | 89 | 185 |
不合格天数 | 4 | 11 | 15 |
合计 | 100 | 100 | 200 |
由表中数据,计算![]() ,
,
![]()
![]() ,
,
∴有90%的把握认为该城市的空气质量指数值与两种方案的选择有关.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】整数集就像一片浩瀚无边的海洋,充满了无尽的奥秘.古希腊数学家毕达哥拉斯发现220和284具有如下性质:220的所有真因数之和恰好等于284,同时284的所有真因数之和也等于220,他把具有这种性质的两个整数叫做一对“亲和数”,“亲和数”的发现吸引了古今中外无数数学爱好者的研究热潮.已知220和284,1184和1210,2924和2620是3对“亲和数”,把这六个数随机分成两组,一组2个数,另一组4个数,则220和284在同一组的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (
(![]() )经过
)经过![]() ,
,![]() 两点.O为坐标原点,且
两点.O为坐标原点,且![]() 的面积为
的面积为![]() .过点
.过点![]() 且斜率为k(
且斜率为k(![]() )的直线l与椭圆C有两个不同的交点M,N,且直线
)的直线l与椭圆C有两个不同的交点M,N,且直线![]() ,
,![]() 分别与y轴交于点S,T.
分别与y轴交于点S,T.
(Ⅰ)求椭圆C的方程;
(Ⅱ)求直线l的斜率k的取值范围;
(Ⅲ)设![]() ,
,![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
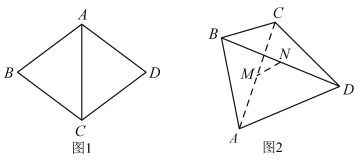
【题目】如图1.四边形![]() 是边长为10的菱形,其对角线
是边长为10的菱形,其对角线![]() ,现将
,现将![]() 沿对角线
沿对角线![]() 折起,连接
折起,连接![]() ,形成如图2的四面体
,形成如图2的四面体![]() ,则异面直线
,则异面直线![]() 与
与![]() 所成角的大小为______.在图2中,设棱
所成角的大小为______.在图2中,设棱![]() 的中点为
的中点为![]() ,
,![]() 的中点为
的中点为![]() ,若四面体
,若四面体![]() 的外接球的球心在四面体的内部,则线段
的外接球的球心在四面体的内部,则线段![]() 长度的取值范围为______.
长度的取值范围为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com