
【题目】已知椭圆C:![]() (
(![]() )经过
)经过![]() ,
,![]() 两点.O为坐标原点,且
两点.O为坐标原点,且![]() 的面积为
的面积为![]() .过点
.过点![]() 且斜率为k(
且斜率为k(![]() )的直线l与椭圆C有两个不同的交点M,N,且直线
)的直线l与椭圆C有两个不同的交点M,N,且直线![]() ,
,![]() 分别与y轴交于点S,T.
分别与y轴交于点S,T.
(Ⅰ)求椭圆C的方程;
(Ⅱ)求直线l的斜率k的取值范围;
(Ⅲ)设![]() ,
,![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ) (Ⅲ)
(Ⅲ)![]()
【解析】
(Ⅰ)把点A坐标代入椭圆的方程得![]() .由
.由![]() 的面积为
的面积为![]() 可知,
可知,![]() ,解得b,进而得椭圆C的方程.
,解得b,进而得椭圆C的方程.
(Ⅱ)设直线l的方程为![]() ,
,![]() ,
,![]() .联立直线l与椭圆C的方程可得关于x的一元二次方程.
.联立直线l与椭圆C的方程可得关于x的一元二次方程.![]() ,进而解得k的取值范围.
,进而解得k的取值范围.
(Ⅲ)因为![]() ,
,![]() ,
,![]() ,
,![]() ,写出直线
,写出直线![]() 的方程,令
的方程,令![]() ,解得
,解得![]() .点S的坐标为
.点S的坐标为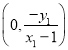 .同理可得:点T的坐标为
.同理可得:点T的坐标为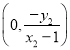 .用坐标表示
.用坐标表示![]() ,
,![]() ,
,![]() ,代入
,代入![]() ,
,![]() ,得
,得![]() .同理
.同理![]() .由(Ⅱ)得
.由(Ⅱ)得![]() ,
,![]() ,代入
,代入![]() ,化简再求取值范围.
,化简再求取值范围.
(Ⅰ)因为椭圆C:![]() 经过点
经过点![]() ,
,
所以![]() 解得
解得![]() .
.
由![]() 的面积为
的面积为![]() 可知,
可知,![]() ,
,
解得![]() ,
,
所以椭圆C的方程为![]() .
.
(Ⅱ)设直线l的方程为![]() ,
,![]() ,
,![]() .
.
联立 ,消y整理可得:
,消y整理可得:![]() .
.
因为直线与椭圆有两个不同的交点,
所以![]() ,解得
,解得![]() .
.
因为![]() ,所以k的取值范围是
,所以k的取值范围是 .
.
(Ⅲ)因为![]() ,
,![]() ,
,![]() ,
,![]() .
.
所以直线![]() 的方程是:
的方程是:![]() .
.
令![]() ,解得
,解得![]() .
.
所以点S的坐标为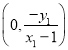 .
.
同理可得:点T的坐标为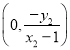 .
.
所以 ,
, ,
,![]() .
.
由![]() ,
,![]() ,
,
可得:![]() ,
,![]() ,
,
所以![]() .
.
同理![]() .
.
由(Ⅱ)得![]() ,
,![]() ,
,
所以
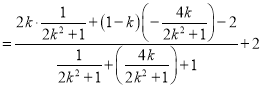
![]()
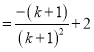

所以![]() 的范围是
的范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】BMI指数(身体质量指数,英文为BodyMassIndex,简称BMI)是衡量人体胖瘦程度的一个标准,BMI=体重(kg)/身高(m)的平方.根据中国肥胖问题工作组标准,当BMI≥28时为肥胖.某地区随机调查了1200名35岁以上成人的身体健康状况,其中有200名高血压患者,被调查者的频率分布直方图如下:
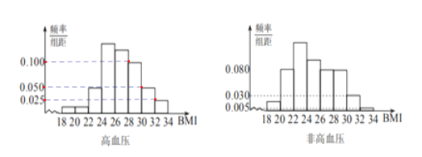
(1)求被调查者中肥胖人群的BMI平均值![]() ;
;
(2)填写下面列联表,并判断是否有99.9%的把握认为35岁以上成人患高血压与肥胖有关.
| 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
肥胖 | 不肥胖 | 合计 | |
高血压 | |||
非高血压 | |||
合计 |
附: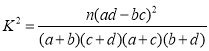 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】农历五月初五是端午节,民间有吃粽子的习惯,粽子又称粽籺,俗称“粽子”,古称“角黍”,是端午节大家都会品尝的食品,传说这是为了纪念战国时期楚国大臣、爱国主义诗人屈原.如图,平行四边形形状的纸片是由六个边长为1的正三角形构成的,将它沿虚线折起来,可以得到如图所示粽子形状的六面体,则该六面体的体积为____;若该六面体内有一球,则该球体积的最大值为____.
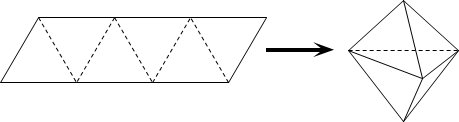
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市先后采用甲、乙两种方案治理空气污染各一年,各自随机抽取一年(365天)内100天的空气质量指数API的检测数据进行分析,若空气质量指数值在[0,300]内为合格,否则为不合格.表1是甲方案检测数据样本的频数分布表,如图是乙方案检测数据样本的频率分布直方图.
表1:
API值 | [0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,300] | 大于300 |
天数 | 9 | 13 | 19 | 30 | 14 | 11 | 4 |
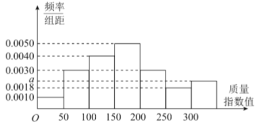
(1)将频率视为概率,求乙方案样本的频率分布直方图中![]() 的值,以及乙方案样本的空气质量不合格天数;
的值,以及乙方案样本的空气质量不合格天数;
(2)求乙方案样木的中位数;
(3)填写下面2×2列联表(如表2),并根据列联表判断是否有90%的把握认为该城市的空气质量指数值与两种方案的选择有关.
表2:
甲方案 | 乙方案 | 合计 | |
合格天数 | _______ | _______ | _______ |
不合格天数 | _______ | _______ | _______ |
合计 | _______ | _______ | _______ |
附: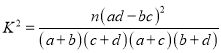
| 0.10 | 0.05 | 0.025 |
| 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为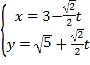 (
(![]() 为参数),在以坐标原点
为参数),在以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴的极坐标中,圆
轴正半轴为极轴的极坐标中,圆![]() 的方程为
的方程为![]() .
.
(1)写出直线![]() 的普通方程和圆
的普通方程和圆![]() 的直角坐标方程;
的直角坐标方程;
(2)若点![]() 的坐标为
的坐标为![]() ,圆
,圆![]() 与直线
与直线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() 的离心率是
的离心率是![]() ,一个顶点是
,一个顶点是![]() .
.

(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设![]() ,
,![]() 是椭圆
是椭圆![]() 上异于点
上异于点![]() 的任意两点,且
的任意两点,且![]() .试问:直线
.试问:直线![]() 是否恒过一定点?若是,求出该定点的坐标;若不是,说明理由.
是否恒过一定点?若是,求出该定点的坐标;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为坐标原点,椭圆
为坐标原点,椭圆![]() 的离心率为
的离心率为![]() ,双曲线
,双曲线![]() 的渐近线与椭圆
的渐近线与椭圆![]() 的交点到原点的距离均为
的交点到原点的距离均为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若点![]() 为椭圆
为椭圆![]() 上的动点,
上的动点,![]() 三点共线,直线
三点共线,直线![]() 的斜率分别为
的斜率分别为![]() .
.
(i)证明:![]() ;
;
(ii)若![]() ,设直线
,设直线![]() 过点
过点![]() ,直线
,直线![]() 过点
过点![]() ,证明:
,证明:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】人们通常以分贝(符号是![]() )为单位来表示声音强度的等级,30~40分贝是较理想的安静环境,超过50分贝就会影响睡眠和休息,70分贝以上会干扰谈话,长期生活在90分贝以上的嗓声环境,会严重影响听力和引起神经衰弱、头疼、血压升高等疾病,如果突然暴露在高达150分贝的噪声环境中,听觉器官会发生急剧外伤,引起鼓膜破裂出血,双耳完全失去听力,为了保护听力,应控制噪声不超过90分贝,一般地,如果强度为
)为单位来表示声音强度的等级,30~40分贝是较理想的安静环境,超过50分贝就会影响睡眠和休息,70分贝以上会干扰谈话,长期生活在90分贝以上的嗓声环境,会严重影响听力和引起神经衰弱、头疼、血压升高等疾病,如果突然暴露在高达150分贝的噪声环境中,听觉器官会发生急剧外伤,引起鼓膜破裂出血,双耳完全失去听力,为了保护听力,应控制噪声不超过90分贝,一般地,如果强度为![]() 的声音对应的等级为
的声音对应的等级为![]() ,则有
,则有![]() ,则
,则![]() 的声音与
的声音与![]() 的声音强度之比为( )
的声音强度之比为( )
A.10B.100C.1000D.10000
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com