
【题目】如图,在三棱柱![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是线段
是线段![]() 的中点.
的中点.
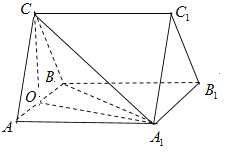
(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)连接![]() ,交
,交![]() 于点
于点![]() ,利用中位线定理可证得
,利用中位线定理可证得![]() ,从而得证;
,从而得证;
(2)以![]() 为原点,
为原点,![]() ,
,![]() ,
,![]() 所在直线分别为
所在直线分别为![]() ,
,![]() ,
,![]() 轴,建立空间直角坐标系,分别求两个面的法向量,利用向量夹角公式求解即可.
轴,建立空间直角坐标系,分别求两个面的法向量,利用向量夹角公式求解即可.
(1)连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,
,
因为棱柱的侧面是平行四边形,所以![]() 是
是![]() 的中点.
的中点.
又因为![]() 是
是![]() 中点,所以
中点,所以![]() 是
是![]() 的中位线.
的中位线.
所以![]() .
.
又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
所以![]() 平面
平面![]() .
.
(2)连接![]() ,
,![]() ,
,![]() .
.
因为![]() ,
,![]() .
.
故![]() ,
,![]() 都为等边三角形.
都为等边三角形.
因为![]() 是
是![]() 中点,所以
中点,所以![]() ,
,![]() ,
,
因为![]() ,
,![]() ,所以
,所以![]() ,
,![]() .
.
所以![]() .
.
所以![]() ,
,![]() ,
,![]() 两两垂直,
两两垂直,
以![]() 为原点,
为原点,![]() ,
,![]() ,
,![]() 所在直线分别为
所在直线分别为![]() ,
,![]() ,
,![]() 轴,建立空间直角坐标系,
轴,建立空间直角坐标系,
则![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
设平面![]() 的法向量
的法向量![]() ,则
,则 ,
,
取![]() ,得
,得![]() ,
,
平面![]() 的法向量
的法向量![]() ,
,
设二面角![]() 的平面角为
的平面角为![]() ,显然
,显然![]() 为锐角,故
为锐角,故 ,
,
所以二面角![]() 的余弦值为
的余弦值为![]() .
.



科目:高中数学 来源: 题型:
【题目】整数集就像一片浩瀚无边的海洋,充满了无尽的奥秘.古希腊数学家毕达哥拉斯发现220和284具有如下性质:220的所有真因数之和恰好等于284,同时284的所有真因数之和也等于220,他把具有这种性质的两个整数叫做一对“亲和数”,“亲和数”的发现吸引了古今中外无数数学爱好者的研究热潮.已知220和284,1184和1210,2924和2620是3对“亲和数”,把这六个数随机分成两组,一组2个数,另一组4个数,则220和284在同一组的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (
(![]() )经过
)经过![]() ,
,![]() 两点.O为坐标原点,且
两点.O为坐标原点,且![]() 的面积为
的面积为![]() .过点
.过点![]() 且斜率为k(
且斜率为k(![]() )的直线l与椭圆C有两个不同的交点M,N,且直线
)的直线l与椭圆C有两个不同的交点M,N,且直线![]() ,
,![]() 分别与y轴交于点S,T.
分别与y轴交于点S,T.
(Ⅰ)求椭圆C的方程;
(Ⅱ)求直线l的斜率k的取值范围;
(Ⅲ)设![]() ,
,![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1.四边形![]() 是边长为10的菱形,其对角线
是边长为10的菱形,其对角线![]() ,现将
,现将![]() 沿对角线
沿对角线![]() 折起,连接
折起,连接![]() ,形成如图2的四面体
,形成如图2的四面体![]() ,则异面直线
,则异面直线![]() 与
与![]() 所成角的大小为______.在图2中,设棱
所成角的大小为______.在图2中,设棱![]() 的中点为
的中点为![]() ,
,![]() 的中点为
的中点为![]() ,若四面体
,若四面体![]() 的外接球的球心在四面体的内部,则线段
的外接球的球心在四面体的内部,则线段![]() 长度的取值范围为______.
长度的取值范围为______.
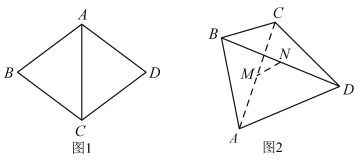
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱ABCD﹣A1B1C1D1中,底面ABCD是矩形,A1D与AD1交于点E,AA1=AD=2AB=4.
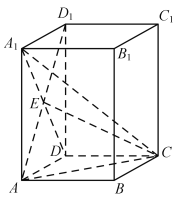
(1)证明:AE⊥平面ECD.
(2)求直线A1C与平面EAC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列选项中说法正确的是( )
A.函数![]() 的单调减区间为
的单调减区间为![]() ;
;
B.命题“![]() ”的否定是“
”的否定是“![]() ”;
”;
C.在三角形![]() 中,“若
中,“若![]() ,则
,则![]() ”的逆否命题是真命题
”的逆否命题是真命题
D.幂函数![]() 过点
过点 ,则
,则![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E:![]() ,直线l不过原点O且不平行于坐标轴,l与E有两个交点A,B,线段AB的中点为M.
,直线l不过原点O且不平行于坐标轴,l与E有两个交点A,B,线段AB的中点为M.
![]() 若
若![]() ,点K在椭圆E上,
,点K在椭圆E上,![]() 、
、![]() 分别为椭圆的两个焦点,求
分别为椭圆的两个焦点,求![]() 的范围;
的范围;
![]() 证明:直线OM的斜率与l的斜率的乘积为定值;
证明:直线OM的斜率与l的斜率的乘积为定值;
![]() 若l过点
若l过点![]() ,射线OM与椭圆E交于点P,四边形OAPB能否为平行四边形?若能,求此时直线l斜率;若不能,说明理由.
,射线OM与椭圆E交于点P,四边形OAPB能否为平行四边形?若能,求此时直线l斜率;若不能,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若关于x的不等式e2x﹣alnx![]() a恒成立,则实数a的取值范围是( )
a恒成立,则实数a的取值范围是( )
A.[0,2e]B.(﹣∞,2e]C.[0,2e2]D.(﹣∞,2e2]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com