
【题目】已知![]() .
.
(Ⅰ)当![]() 时,求
时,求![]() 的单调区间;
的单调区间;
(Ⅱ)设![]() 是
是![]() 的极小值点,求
的极小值点,求![]() 的最大值.
的最大值.
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (
(![]() )的离心率为
)的离心率为![]() ,且椭圆C的中心O关于直线
,且椭圆C的中心O关于直线![]() 的对称点落在直线
的对称点落在直线![]() 上.
上.
(1)求椭圆C的方程;
(2)设P![]() ,M、N是椭圆C上关于x轴对称的任意两点,连接
,M、N是椭圆C上关于x轴对称的任意两点,连接![]() 交椭圆C于另一点E,求直线
交椭圆C于另一点E,求直线![]() 的斜率取值范围,并证明直线
的斜率取值范围,并证明直线![]() 与x轴相交于定点.
与x轴相交于定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年新型冠状病毒疫情爆发,贵州省教育厅号召全体学生“停课不停学”.自
年新型冠状病毒疫情爆发,贵州省教育厅号召全体学生“停课不停学”.自![]() 月
月![]() 日起,高三年级学生通过收看“阳光校园·空中黔课”进行线上网络学习.为了检测线上网络学习效果,某中学随机抽取
日起,高三年级学生通过收看“阳光校园·空中黔课”进行线上网络学习.为了检测线上网络学习效果,某中学随机抽取![]() 名高三年级学生做“是否准时提交作业”的问卷调查,并组织了一场线上测试,调查发现有
名高三年级学生做“是否准时提交作业”的问卷调查,并组织了一场线上测试,调查发现有![]() 名学生每天准时提交作业,根据他们的线上测试成绩得频率分布直方图(如图
名学生每天准时提交作业,根据他们的线上测试成绩得频率分布直方图(如图![]() 所示);另外
所示);另外![]() 名学生偶尔没有准时提交作业,根据他们的线上测试成绩得茎叶图(如图
名学生偶尔没有准时提交作业,根据他们的线上测试成绩得茎叶图(如图![]() 所示,单位:分)
所示,单位:分)
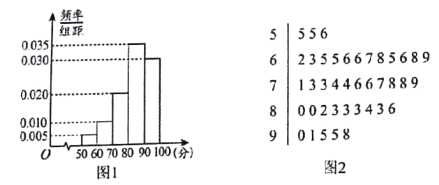
(1)成绩不低于![]() 分为
分为![]() 等,低于
等,低于![]() 分为非
分为非![]() 等.完成以下列联表,并判断是否有
等.完成以下列联表,并判断是否有![]() 以上的把握认为成绩取得
以上的把握认为成绩取得![]() 等与每天准时提交作业有关?
等与每天准时提交作业有关?
准时提交作业与成绩等次列联表 | 单位:人 | ||
A等 | 非A等 | 合计 | |
每天准时提交作业 | |||
偶尔没有准时提交作业 | |||
合计 | |||
(2)成绩低于![]() 分为不合格,从这
分为不合格,从这![]() 名学生里成绩不合格的学生中再抽取
名学生里成绩不合格的学生中再抽取![]() 人,其中每天准时提交作业的学生人数为
人,其中每天准时提交作业的学生人数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
附: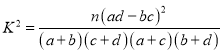
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,点![]() 的极坐标是
的极坐标是![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() .以极点为坐标原点,极轴为
.以极点为坐标原点,极轴为![]() 轴的正半轴建立平面直角坐标系,斜率为
轴的正半轴建立平面直角坐标系,斜率为![]() 的直线
的直线![]() 经过点
经过点![]() .
.
(1)若![]() 时,写出直线
时,写出直线![]() 和曲线
和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 和曲线
和曲线![]() 相交于不同的两点
相交于不同的两点![]() ,求线段
,求线段![]() 的中点
的中点![]() 的在直角坐标系中的轨迹方程.
的在直角坐标系中的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阅读下列材料,回答所提问题:设函数![]() ,①
,①![]() 的定义域为
的定义域为![]() ,其图像是一条连续不断的曲线;②
,其图像是一条连续不断的曲线;②![]() 是偶函数;③
是偶函数;③![]() 在
在![]() 上不是单调函数;④
上不是单调函数;④![]() 恰有
恰有![]() 个零点,写出符合上述①②④条件的一个函数的解析式是______;写出符合上述所有条件的一个函数的解析式是______.
个零点,写出符合上述①②④条件的一个函数的解析式是______;写出符合上述所有条件的一个函数的解析式是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】BMI指数(身体质量指数,英文为BodyMassIndex,简称BMI)是衡量人体胖瘦程度的一个标准,BMI=体重(kg)/身高(m)的平方.根据中国肥胖问题工作组标准,当BMI≥28时为肥胖.某地区随机调查了1200名35岁以上成人的身体健康状况,其中有200名高血压患者,被调查者的频率分布直方图如下:
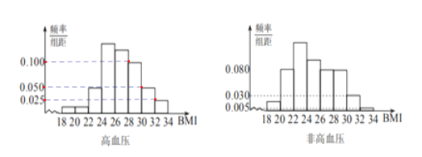
(1)求被调查者中肥胖人群的BMI平均值![]() ;
;
(2)填写下面列联表,并判断是否有99.9%的把握认为35岁以上成人患高血压与肥胖有关.
| 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
肥胖 | 不肥胖 | 合计 | |
高血压 | |||
非高血压 | |||
合计 |
附: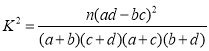 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四面体ABCD中,△ABC和△BCD均是边长为1的等边三角形,已知四面体ABCD的四个顶点都在同一球面上,且AD是该球的直径,则四面体ABCD的体积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市先后采用甲、乙两种方案治理空气污染各一年,各自随机抽取一年(365天)内100天的空气质量指数API的检测数据进行分析,若空气质量指数值在[0,300]内为合格,否则为不合格.表1是甲方案检测数据样本的频数分布表,如图是乙方案检测数据样本的频率分布直方图.
表1:
API值 | [0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,300] | 大于300 |
天数 | 9 | 13 | 19 | 30 | 14 | 11 | 4 |
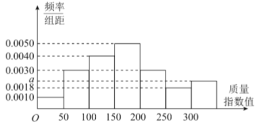
(1)将频率视为概率,求乙方案样本的频率分布直方图中![]() 的值,以及乙方案样本的空气质量不合格天数;
的值,以及乙方案样本的空气质量不合格天数;
(2)求乙方案样木的中位数;
(3)填写下面2×2列联表(如表2),并根据列联表判断是否有90%的把握认为该城市的空气质量指数值与两种方案的选择有关.
表2:
甲方案 | 乙方案 | 合计 | |
合格天数 | _______ | _______ | _______ |
不合格天数 | _______ | _______ | _______ |
合计 | _______ | _______ | _______ |
附: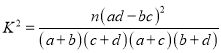
| 0.10 | 0.05 | 0.025 |
| 2.706 | 3.841 | 5.024 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com