
分析 (Ⅰ)求出函数的导数,计算f(1),f′(1)的值,求出切线方程即可;
(Ⅱ)求出函数的导数,求出b的值,通过讨论a的范围求出函数的单调区间即可;
(Ⅲ)问题转化为方程b+1=$\frac{lnx}{x}$在(0,+∞)有2个不同的根,设g(x)=$\frac{lnx}{x}$(x>0),根据函数的单调性求出b的范围即可.
解答 解:(Ⅰ)a=2,b=1时,f(x)=2lnx-3x+x2,
∴f′(x)=$\frac{2}{x}$-3+2x,∴f′(1)=1,f(1)=-2,
故f(x)在x=1处的切线方程是x-y-3=0;
(Ⅱ)f′(x)=$\frac{a}{x}$-(a+b)+2x,
由f(x)在x=1处取得极值,得f′(1)=0,解得:b=2,
故f′(x)=$\frac{a}{x}$-(a+2)+2x=$\frac{2(x-\frac{a}{2})(x-1)}{x}$,
a=2时,f′(x)≥0,不满足f(x)在x=1处取得极值,故a≠2,
①a≤0时,x∈(0,1)时,f′(x)<0,x∈(1,+∞)时,f′(x)>0,
故f(x)在(0,1)递减,在(1,+∞)递增;
②0<$\frac{a}{2}$<1即0<a<2时,0<x<$\frac{a}{2}$或x>1时,f′(x)>0,$\frac{a}{2}$<x<1时,f′(x)<0,
故f(x)在(0,$\frac{a}{2}$),(1,+∞)递增,在($\frac{a}{2}$,1)递减;
③a>2时,0<x<1或x>$\frac{a}{2}$时,f′(x)>0,1<x<$\frac{a}{2}$时,f′(x)<0,
故f(x)在(0,1),($\frac{a}{2}$,+∞)递增,在(1,$\frac{a}{2}$)递减;
(Ⅲ)a=1时,函数φ(x)=f(x)-x2=lnx-(1+b)x,
φ(x)有2个不同的零点x1,x2,
即方程b+1=$\frac{lnx}{x}$在(0,+∞)有2个不同的根,
设g(x)=$\frac{lnx}{x}$(x>0),则g′(x)=$\frac{1-lnx}{{x}^{2}}$,
x∈(0,e)时,g′(x)>0,x∈(e,+∞)时,g′(x)<0,
故g(x)在(0,e)递增,在(e,+∞)递减,
故x=e时,g(x)max=g(e)=$\frac{1}{e}$,
∵g(1)=0,x∈(0,1)时,g(x)<0,x∈(1,+∞)时,g(x)>0,
故0<b+1<$\frac{1}{e}$,b的范围是(-1,$\frac{1}{e}$-1).
点评 本题考查了切线方程问题,考查函数的单调性、最值问题,考查导数的应用以及分类讨论思想,转化思想,是一道综合题.


科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 6 | C. | 12 | D. | 24 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
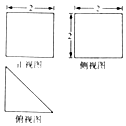 在《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称为阳马,将四个面都为直角三角形的四面体称为鳖臑,某几何体τ的三视图如图所示,将该几何体分别沿棱和表面的对角线截开可得到到一个鳖臑和一个阳马,设V表示体积,则Vτ的外接球:V阳马:V鳖臑=( )
在《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称为阳马,将四个面都为直角三角形的四面体称为鳖臑,某几何体τ的三视图如图所示,将该几何体分别沿棱和表面的对角线截开可得到到一个鳖臑和一个阳马,设V表示体积,则Vτ的外接球:V阳马:V鳖臑=( )| A. | 9π:2:1 | B. | 3$\sqrt{3}$π:3:1 | C. | 3$\sqrt{3}$π:2:1 | D. | 3$\sqrt{3}$π:1:1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m∥α且n∥α,则m∥n | B. | 若m⊥β且m⊥n,则n∥β | ||
| C. | 若m⊥α且m∥β,则α⊥β | D. | 若α⊥β且m⊥α,m⊥n则n⊥β |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
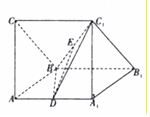 在如图所示的直三棱柱ABC-A1B1C1中,面AA1B1B和面AA1C1C都是边长为1的正方形且互相垂直,D为AA1的中点,E为BC1的中点.
在如图所示的直三棱柱ABC-A1B1C1中,面AA1B1B和面AA1C1C都是边长为1的正方形且互相垂直,D为AA1的中点,E为BC1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2017}$ | B. | $\frac{2π}{2017}$ | C. | $\frac{4π}{2017}$ | D. | $\frac{π}{4034}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com