
 .记动点C的轨迹为曲线W.
.记动点C的轨迹为曲线W. )且斜率为k的直线l与曲线W 有两个不同的交点P和Q,是否存在常数k,使得向量
)且斜率为k的直线l与曲线W 有两个不同的交点P和Q,是否存在常数k,使得向量 +
+ 与向量
与向量 共线?如果存在,求出k的值;如果不存在,请说明理由.
共线?如果存在,求出k的值;如果不存在,请说明理由. y+8=0上.当∠F1RF2取最大值时,求
y+8=0上.当∠F1RF2取最大值时,求 的值.
的值. +y2=1(y≠0).
+y2=1(y≠0). ,代入椭圆方程,得
,代入椭圆方程,得 +(kx+
+(kx+ )2=1.
)2=1. +k2)x2+2
+k2)x2+2 kx+1=0.①
kx+1=0.① +k2)=4k2-2>0,解得k<-
+k2)=4k2-2>0,解得k<- 或k>
或k> .
. +
+ =(x1+x2,y1+y2),
=(x1+x2,y1+y2),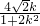 .②
.② ③
③ +
+ 与向量(-2,1)共线等价于x1+x2=-
与向量(-2,1)共线等价于x1+x2=- (y1+y2),
(y1+y2), .
. +
+ 与
与 共线
共线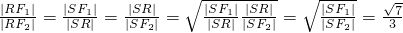 .
. ,代入椭圆方程,得(
,代入椭圆方程,得( +k2)x2+2
+k2)x2+2 kx+1=0.因为直线l与椭圆有两个不同的交点,所以△=8k2-4(
kx+1=0.因为直线l与椭圆有两个不同的交点,所以△=8k2-4( +k2)=4k2-2>0,解得k<-
+k2)=4k2-2>0,解得k<- 或k>
或k> .设P(x1,y1),Q(x2,y2),则
.设P(x1,y1),Q(x2,y2),则 +
+ =(x1+x2,y1+y2),x1+x2,=-
=(x1+x2,y1+y2),x1+x2,=-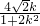 .y1+y2=k(x1+x2)+2
.y1+y2=k(x1+x2)+2 .所以
.所以 +
+ 与向量(-2,1)共线等价于x1+x2=-
与向量(-2,1)共线等价于x1+x2=- (y1+y2),由此能够推导出不存在常数k,使得向量
(y1+y2),由此能够推导出不存在常数k,使得向量 +
+ 与
与 共线.
共线. 的值.
的值.

 名师点拨卷系列答案
名师点拨卷系列答案科目:高中数学 来源: 题型:
 如图,已知点A(-1,0)与点B(1,0),C是圆x2+y2=1上的动点,连接BC并延长至D,使得|CD|=|BC|,求AC与OD的交点P的轨迹方程.
如图,已知点A(-1,0)与点B(1,0),C是圆x2+y2=1上的动点,连接BC并延长至D,使得|CD|=|BC|,求AC与OD的交点P的轨迹方程.查看答案和解析>>
科目:高中数学 来源: 题型:
| OPn |
| OA |
| OB |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com