练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    8．点A（-1，$\sqrt{3}$），B（1，3$\sqrt{3}$），则直线AB的倾斜角为（　　）
    A．30°B．150°C．60°D．120°

    分析 设直线AB的倾斜角为θ，则θ∈[0°，180°）．则kAB=$\sqrt{3}$=tanθ，即可得出．

    解答 解：设直线AB的倾斜角为θ，则θ∈[0°，180°）．
    则kAB=$\frac{3\sqrt{3}-\sqrt{3}}{1-（-1）}$=$\sqrt{3}$=tanθ，
    ∴θ=60°．
    故选：C．

    点评 本题考查了直线的斜率与倾斜角的关系，考查了推理能力与计算能力，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    18．数列{an}的前n项和为Sn，已知a1=1，且an+1=λSn-Sn+1，其中λ是常数，若{an}是递增数列，则λ的取值范围是λ＞3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

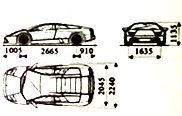    19．髙先生新购买了辆小汽车，汽车的一些参数如图所示（单位：毫米），他计划把车放在车库地面的中间，四周边缘外前后左右各留半米且上方留空一米，则该车库的体积（保留小数点后两位数字）至少为（　　）
    A．11.64立方米B．36.28立方米C．38.60立方米D．40.70立方米

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．已知p是“?x＞0，使f（x）=x+$\frac{|a-3|}{x}$的值小于2”的否定．q是“g（x）=ax2-2x在[$\frac{1}{4}$，$\frac{1}{2}$]上单调”，则p是q的（　　）
    A．充分不必要B．必要不充分
    C．充要D．既不充分也不必要

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知集合A={x|y=lg（1-x）}，B是函数f（x）=-x2+2x+m（m∈R）的值域．
    （1）分别用区间表示集合A，B；
    （2）当A∩B=A时，求m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．若变量x，y满足约束条件$\left\{\begin{array}{l}{y≤x}\\{x+y≤1}\\{y≥-1}\end{array}\right.$，且z=2x+y的最大值和最小值分别为m和n，则n-m=（　　）
    A．-5B．-6C．5D．6

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．数列{an}中，a1=1，an=a1+$\frac{1}{2}$a2+$\frac{1}{3}$a3…+$\frac{1}{n-1}$an-1，（n≥2，n∈N*），若ak=100，则k=200．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．三人踢毯子，互相传递，每人每次只能踢一下，若由甲开始踢，经过4次传递后，毽子又被踢回甲，则不同的传递方式共有（　　）
    A．4种B．5种C．6种D．12种

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．已知函数f（x）=$\left\{\begin{array}{l}{x+1，x≥0}\\{x-2，x＜0}\end{array}\right.$，求f（-3），f（1），f（0），f（$\frac{3}{2}$）．

    查看答案和解析>>

    同步练习册答案