
分析 由已知数列递推式可得an+1=a1+$\frac{1}{2}$a2+$\frac{1}{3}$a3…+$\frac{1}{n-1}$an-1+$\frac{1}{n}{a}_{n}$,作差后即可得到$\frac{{a}_{n+1}}{n+1}=\frac{{a}_{n}}{n}$(n≥2),再由已知求出a2,则数列在n≥2时的通项公式可求,由ak=100求得k值.
解答 解:由an=a1+$\frac{1}{2}$a2+$\frac{1}{3}$a3…+$\frac{1}{n-1}$an-1,(n≥2,n∈N*),得
an+1=a1+$\frac{1}{2}$a2+$\frac{1}{3}$a3…+$\frac{1}{n-1}$an-1+$\frac{1}{n}{a}_{n}$,
两式作差得:${a}_{n+1}-{a}_{n}=\frac{1}{n}{a}_{n}$(n≥2),
∴${a}_{n+1}=\frac{n+1}{n}{a}_{n}$,
∴$\frac{{a}_{n+1}}{n+1}=\frac{{a}_{n}}{n}$(n≥2),
由a1=1,an=a1+$\frac{1}{2}$a2+$\frac{1}{3}$a3…+$\frac{1}{n-1}$an-1,得a2=a1=1,
∴当n≥2时,$\frac{{a}_{n}}{n}=\frac{{a}_{2}}{2}=\frac{1}{2}$,${a}_{n}=\frac{n}{2}$,
由ak=100=$\frac{k}{2}$,得k=200.
故答案为:200.
点评 本题考查数列递推式,考查了作差法求数列的通项公式,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | $\frac{11}{5}$ | D. | $\frac{37}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m?α,n?α,m∥β,n∥β,则α∥β | B. | 若m∥n,n∥α,则m∥α | ||
| C. | 若m⊥α,n⊥α,则m∥n | D. | 若α⊥γ,β⊥γ,则α∥β |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 150° | C. | 60° | D. | 120° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 互斥但非对立事件 | B. | 对立事件 | ||
| C. | 相互独立事件 | D. | 以上都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
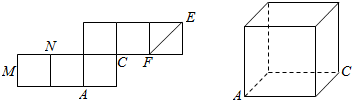 如图,是一个正方体的平面展开图及该正方形的直观图的示意图,其中M是所在棱的中点
如图,是一个正方体的平面展开图及该正方形的直观图的示意图,其中M是所在棱的中点查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com