Question

10．已知抛物线y²=4x的焦点为F，A（-1，0），点P是抛物线上的动点，则当$\frac{{|{PF}|}}{{|{PA}|}}$的值最小时，△PAF的面积为（　　）

• A． $\frac{{\sqrt{2}}}{2}$
• B． 2
• C． 2$\sqrt{2}$
• D． 4

Answer 1

分析 设P到准线的距离为PQ，根据抛物线的性质可知$\frac{|PF|}{|PA|}=\frac{|PQ|}{|PA|}$=sin∠PAQ．从而当∠PAQ最小，即AP与抛物线相切时，$\frac{{|{PF}|}}{{|{PA}|}}$的值最小．利用解方程组的方程求出抛物线过A点的切线方程得出P点坐标，代入面积公式得出面积．

解答 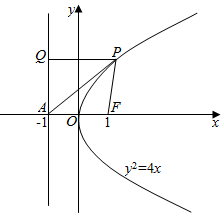解：抛物线的准线方程为x=-1．
设P到准线的距离为|PQ|，则|PQ|=|PF|．
∴$\frac{|PF|}{|PA|}=\frac{|PQ|}{|PA|}$=sin∠PAQ．
∴当PA与抛物线y²=4x相切时，∠PAQ最小，即$\frac{{|{PF}|}}{{|{PA}|}}$取得最小值．
设过A点的直线y=kx+k与抛物线相切（k≠0），代入抛物线方程得k²x²+（2k²-4）x+k²=0，
∴△=（2k²-4）²-4k⁴=0，解得k=±1．
即x²-2x+1=0，解得x=1，把x=1代入y²=4x得y=±2．
∴P（1，2）或P（1，-2）．
∴S_△PAF=$\frac{1}{2}|AF|•|{y}_{P}|$=$\frac{1}{2}×2×2$=2．
故选：B．

点评 本题考查了抛物线的性质，直线与圆锥曲线的位置关系属于中档题．