
| A. | qx+3y+p=0 | B. | qx-3y+p=0 | C. | px+3y+q=0 | D. | px-3y+q=0 |
分析 分别设出A和B的坐标,根据抛物线上两点的横坐标都是方程的解得到方程有两个不等的实数根,即△>0,列出p与q的关系式,在这个关系式成立时,分别把A和B的坐标代入抛物线解析式和方程中,分别消去平方项,根据两等式的特点即可得到直线AB的方程.
解答 解:设A(x1,y1),B(x2,y2),且方程有两个不同的解得到:△=p2-4q>0,
把A的坐标代入抛物线解析式和已知的方程得:x12=3y1①,x12+px1+q=0②,
①-②整理得:px1+3y1+q=0③;
同理把B的坐标代入抛物线解析式和已知的方程,化简可得:px2+3y2+q=0④,
③④表示经过A和B的方程,所以直线AB的方程是:px+3y+q=0(△=p2-4q>0).
故答案选:C.
点评 本题考查学生会求动点的轨迹方程,掌握一元二次方程有两个不相等的实数根的条件为△>0,是一道综合题,考查学生分析解决问题的能力,属于中档题.


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:选择题
| A. | 72n+1 | B. | 22n+1 | C. | 32n+1 | D. | 52n+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
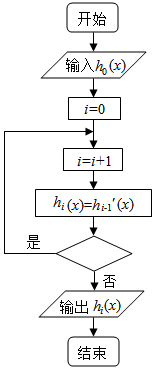 在如图所示的程序框图中(其中hi-1′(x)表示hi-1的导函数),当输入h0(x)=xex时,输出的hi(x)的结果是(x+2016)ex,则程序框图中的判断框内应填入( )
在如图所示的程序框图中(其中hi-1′(x)表示hi-1的导函数),当输入h0(x)=xex时,输出的hi(x)的结果是(x+2016)ex,则程序框图中的判断框内应填入( )| A. | i≤2014? | B. | i≤2015? | C. | i≤2016? | D. | i≤2017? |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 20、8 | B. | 24、10 | C. | 10.5、24.5 | D. | 24.5、10.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
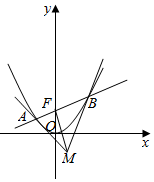 如图,已知F是抛物线x2=2py(p>0)的焦点,O为坐标原点,过点O、F的圆的圆心为Q,点Q到抛物线准线的距离为$\frac{3}{2}$.过点F的直线l交抛物线于A,B两点,过A,B分别作抛物线的切线,两切线交点为M.
如图,已知F是抛物线x2=2py(p>0)的焦点,O为坐标原点,过点O、F的圆的圆心为Q,点Q到抛物线准线的距离为$\frac{3}{2}$.过点F的直线l交抛物线于A,B两点,过A,B分别作抛物线的切线,两切线交点为M.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com