
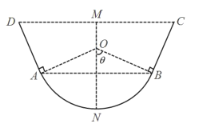
【题目】某农场计划设计建造一条2000米长的水渠,其横断面如图所示.其中,底部是半径为1米的圆弧![]() ,上部是有一定倾角的线段
,上部是有一定倾角的线段![]() 与
与![]() ,渠深
,渠深![]() 为
为![]() 米,且圆弧
米,且圆弧![]() 的圆心为O在
的圆心为O在![]() 上,
上,![]() ,
,![]() ,
,![]() ,
,![]() .据测算,水渠底部曲面每平方米的造价为
.据测算,水渠底部曲面每平方米的造价为![]() 百元,上部矩形壁面每平方米的造价为1百元,其他费用忽略不计.设
百元,上部矩形壁面每平方米的造价为1百元,其他费用忽略不计.设![]() ,
,![]() .
.
(1)试用![]() 表示水渠建造的总费用
表示水渠建造的总费用![]() (单位:百元);
(单位:百元);
(2)试确定![]() 的值,使得建造总费用最低.
的值,使得建造总费用最低.
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源: 题型:
【题目】某公司生产的某种产品,如果年返修率不超过千分之一,则其生产部门当年考核优秀,现获得该公司2011-2018年的相关数据如下表所示:
年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年生产台数(万台) | 2 | 3 | 4 | 5 | 6 | 7 | 10 | 11 |
该产品的年利润(百万元) | 2.1 | 2.75 | 3.5 | 3.25 | 3 | 4.9 | 6 | 6.5 |
年返修台数(台) | 21 | 22 | 28 | 65 | 80 | 65 | 84 | 88 |
部分计算结果:
| ||||||||
注:年返修率=![]()
(1)从该公司2011-2018年的相关数据中任意选取3年的数据,以![]() 表示3年中生产部门获得考核优秀的次数,求
表示3年中生产部门获得考核优秀的次数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)根据散点图发现2015年数据偏差较大,如果去掉该年的数据,试用剩下的数据求出年利润![]() (百万元)关于年生产台数
(百万元)关于年生产台数![]() (万台)的线性回归方程(精确到0.01).
(万台)的线性回归方程(精确到0.01).
附:线性回归方程![]() 中,
中,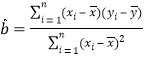
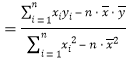 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校高一年级学生某次身体素质体能测试的原始成绩采用百分制,已知所有这些学生的原始成绩均分布在![]() 内,发布成绩使用等级制.各等级划分标准见下表.
内,发布成绩使用等级制.各等级划分标准见下表.
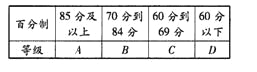
规定:![]() 三级为合格等级,D为不合格等级.为了解该校高一年级学生身体素质情况,从中抽取了
三级为合格等级,D为不合格等级.为了解该校高一年级学生身体素质情况,从中抽取了![]() 名学生的原始成绩作为样本进行统计.按照
名学生的原始成绩作为样本进行统计.按照![]() 的分组作出频率分布直方图如图1所示,样本中分数在80分及以上的所有数据的茎叶图如图2所示.
的分组作出频率分布直方图如图1所示,样本中分数在80分及以上的所有数据的茎叶图如图2所示.
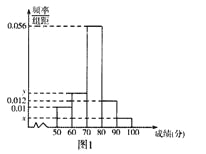
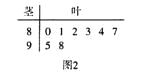
(I)求![]() 和频率分布直方图中的
和频率分布直方图中的![]() 的值,并估计该校高一年级学生成绩是合格等级的概率;
的值,并估计该校高一年级学生成绩是合格等级的概率;
(II)在选取的样本中,从![]() 两个等级的学生中随机抽取2名学生进行调研,求至少有一名学生是
两个等级的学生中随机抽取2名学生进行调研,求至少有一名学生是![]() 等级的概率.
等级的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,过
,过![]() ,
,![]() 分别作
分别作![]() 的垂线,垂足分别为
的垂线,垂足分别为![]() ,
,![]() ,已知
,已知![]() ,
,![]() ,将梯形
,将梯形![]() 沿
沿![]() ,
,![]() 同侧折起,使得平面
同侧折起,使得平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,得到图2.
,得到图2.
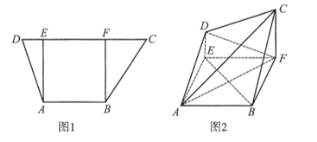
(1)证明:![]() 平面
平面![]() ;
;
(2)求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】进入12月以来,某地区为了防止出现重污染天气,坚持保民生、保蓝天,严格落实机动车限行等一系列“管控令”,该地区交通管理部门为了了解市民对“单双号限行”的赞同情况,随机采访了220名市民,将他们的意见和是否拥有私家车情况进行了统计,得到如下的2×2列联表:
| 赞同限行 | 不赞同限行 | 合计 |
没有私家车 | 90 | 20 | 110 |
有私家车 | 70 | 40 | 110 |
合计 | 160 | 60 | 220 |
(1)根据上面的列联表判断,能否有99%的把握认为“赞同限行与是否拥有私家车”有关;
(2)为了解限行之后是否对交通拥堵、环境污染起到改善作用,从上述调查的不赞同限行的人员中按分层抽样抽取6人,再从这6人中随机抽出2名进行电话回访,求抽到的2人中至少有1名“没有私家车”人员的概率.
参考公式:K2=![]()
P(K2≥k) | 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
k | 2.706 | 3..841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,有四座城市![]() 、
、![]() 、
、![]() 、
、![]() ,其中
,其中![]() 在
在![]() 的正东方向,且与
的正东方向,且与![]() 相距
相距![]() ,
,![]() 在
在![]() 的北偏东
的北偏东![]() 方向,且与
方向,且与![]() 相距
相距![]() ;
;![]() 在
在![]() 的北偏东
的北偏东![]() 方向,且与
方向,且与![]() 相距
相距![]() ,一架飞机从城市
,一架飞机从城市![]() 出发以
出发以![]() 的速度向城市
的速度向城市![]() 飞行,飞行了
飞行,飞行了![]() ,接到命令改变航向,飞向城市
,接到命令改变航向,飞向城市![]() ,此时飞机距离城市
,此时飞机距离城市![]() 有( )
有( )
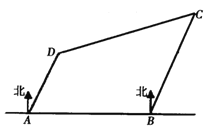
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com