
| A. | $\frac{8}{9}$ | B. | $\frac{4}{9}$ | C. | $\frac{8}{3}$ | D. | $\frac{4}{3}$ |
分析 根据向量的加减的几何意义和数量积定义即可.
解答 解:∵AD=BE=2,且$\overrightarrow{AD}$、$\overrightarrow{EB}$的夹角为$\frac{2π}{3}$,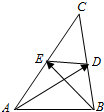
∴$\overrightarrow{AD}$•$\overrightarrow{EB}$=|$\overrightarrow{AD}$|•|$\overrightarrow{EB}$|cos$\frac{2π}{3}$=2×2×(-$\frac{1}{2}$)=-2,
∵AD,BE分别是△ABC的中线,
∴$\overrightarrow{AD}$=$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AC}$),$\overrightarrow{BE}$=$\frac{1}{2}$($\overrightarrow{BA}$+$\overrightarrow{BC}$)=$\frac{1}{2}$($\overrightarrow{AC}$-$\overrightarrow{AB}$-$\overrightarrow{AB}$)=$\frac{1}{2}$$\overrightarrow{AC}$-$\overrightarrow{AB}$,
∴$\overrightarrow{AB}$=$\frac{2}{3}$($\overrightarrow{AD}$-$\overrightarrow{BE}$),$\overrightarrow{AC}$=$\frac{2}{3}$(2$\overrightarrow{AD}$+$\overrightarrow{BE}$),
∴$\overrightarrow{AB}$•$\overrightarrow{AC}$=$\frac{4}{9}$($\overrightarrow{AD}$-$\overrightarrow{BE}$)(2$\overrightarrow{AD}$+$\overrightarrow{BE}$)=$\frac{4}{9}$(2${\overrightarrow{AD}}^{2}$-$\overrightarrow{AD}$•$\overrightarrow{BE}$-${\overrightarrow{BE}}^{2}$)=$\frac{4}{9}$(8-2-4)=$\frac{8}{9}$,
故选:A.
点评 本题考查了数量积定义及其平行四边形法则、三角形法则等基础知识与基本技能方法,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)有最大值7 | B. | 函数f(x)有最小值7 | C. | 函数f(x)有最小值4 | D. | 函数f(x)有最大值4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$过点P(1,$\frac{3}{2}$),其左、右焦点分别为F1,F2,离心率e=$\frac{1}{2}$,M,N是直线x=4上的两个动点,且$\overrightarrow{{F_1}M}$•$\overrightarrow{{F_2}N}$=0.
如图,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$过点P(1,$\frac{3}{2}$),其左、右焦点分别为F1,F2,离心率e=$\frac{1}{2}$,M,N是直线x=4上的两个动点,且$\overrightarrow{{F_1}M}$•$\overrightarrow{{F_2}N}$=0.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在平面直角坐标系xOy中,以Ox轴为始边作两个锐角α、β,它们的终边分别与单位圆相交于A、B两点,已知A、B的纵坐标分别为$\frac{{\sqrt{10}}}{10}$,$\frac{{\sqrt{2}}}{10}$.
如图,在平面直角坐标系xOy中,以Ox轴为始边作两个锐角α、β,它们的终边分别与单位圆相交于A、B两点,已知A、B的纵坐标分别为$\frac{{\sqrt{10}}}{10}$,$\frac{{\sqrt{2}}}{10}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图是一个正方体的平面展开图,在这个正方体中
如图是一个正方体的平面展开图,在这个正方体中| A. | ①②③ | B. | ②④ | C. | ③④ | D. | ②③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com