
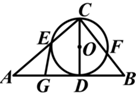 如图,已知CD是△ABC中AB边上的高,以CD为直径的⊙O分别交CA、CB于点E、F,点G是AD的中点.$GE=BD=2,EC=\frac{9}{5}$.
如图,已知CD是△ABC中AB边上的高,以CD为直径的⊙O分别交CA、CB于点E、F,点G是AD的中点.$GE=BD=2,EC=\frac{9}{5}$.分析 (1)连接OE,由CD是⊙O直径,证得∠OED=∠ODE,在Rt△AED中,G为AD中点,得出$EG=GD=\frac{1}{2}AD$,∠GED=∠GDE,求得∠OEG=∠DEO+∠GED=∠ODE+∠GDE=∠GDC=90°,即可得出结论;
(2)连接OG,证得△ADC∽△AED,得出$\frac{AD}{AC}=\frac{AE}{AD}$,解得AE的长与AC的长,由勾股定理得:DC、BC的长,即可求得sin∠DCB.
解答 (1)证明:连接OE,如图所示:
∵CD是⊙O的直径,
∴∠CED=90°,
∴∠AED=90°,
∵OE=OD,
∴∠OED=∠ODE,
在Rt△AED中,
∵G为AD中点,
∴$EG=GD=\frac{1}{2}AD$,
∴∠GED=∠GDE,
∵CD是△ABC中AB边上的高,
∴∠GDC=90°,
∴∠OEG=∠DEO+∠GED=∠ODE+∠GDE=∠GDC=90°,
∴GE是⊙O的切线;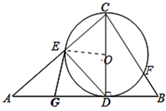
(2)解:连接OG,如图所示:
由(1)得:AD=2GE=4,
∵∠ADC=∠AED=90°,∠EAD=∠DAC,
∴△ADC∽△AED,
∴$\frac{AD}{AC}=\frac{AE}{AD}$,
∴AD2=AE•AC,
即${4^2}=AE({AE+\frac{9}{5}})$,
解得:$AE=\frac{16}{5}$或AE=-5(不合题意,舍去),
∴$AC=\frac{16}{5}+\frac{9}{5}=5$,
由勾股定理得:$DC=\sqrt{A{C^2}-A{D^2}}=\sqrt{{5^2}-{4^2}}=3$,
由勾股定理得:$BC=\sqrt{B{D^2}+C{D^2}}=\sqrt{{2^2}+{3^2}}=\sqrt{13}$,
∴$sin∠DCB=\frac{BD}{BC}=\frac{2}{{\sqrt{13}}}=\frac{{2\sqrt{13}}}{13}$.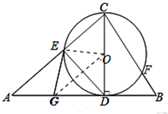
点评 本题考查了圆周角定理、切线的判定、相似三角形的判定与性质、勾股定理、三角函数等知识;本题综合性强,有一定难度.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | b<0<a | B. | 0<a<b | C. | b<a<0 | D. | -1<b<0<a<1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M∩N={ 4,6 } | B. | M∪N=U | C. | (∁UN )∪M=U | D. | (∁UM)∩N=N |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x>0,cosx+sinx>1 | B. | ?x0≤0,cosx0+sinx0≤1 | ||
| C. | ?x>0,cosx+sinx≤1 | D. | ?x0>0,cosx0+sinx0≤1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com