
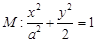
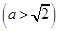 的右焦点为
的右焦点为 ,直线
,直线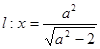 与
与 轴交于点
轴交于点 ,若
,若 (其中
(其中 为坐标原点).
为坐标原点). 的方程;
的方程;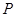 是椭圆
是椭圆 上的任意一点,
上的任意一点,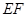 为圆
为圆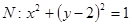 的任意一条直径(
的任意一条直径(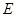 、
、 为直径的两个端点),求
为直径的两个端点),求 的最大值.
的最大值. 的方程为
的方程为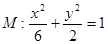 . (2)
. (2) 的最大值为11.
的最大值为11. 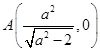 ,
,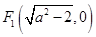 ,由
,由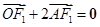 ,得
,得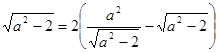 ,从而得到关于a的方程,求出a值.
,从而得到关于a的方程,求出a值.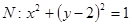 的圆心为
的圆心为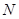 ,则
,则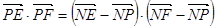

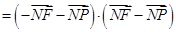
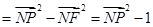 ,
, 的最大值转化为求
的最大值转化为求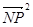 的最大值,再利用两点间的距离公式再借助P在椭圆上,可以把
的最大值,再利用两点间的距离公式再借助P在椭圆上,可以把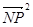 转化为关于P的横坐标x的函数问题来解决.
转化为关于P的横坐标x的函数问题来解决.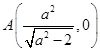 ,
,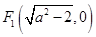 ,………………………1分
,………………………1分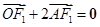 ,得
,得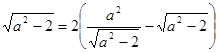 .………………3分
.………………3分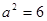 .所以椭圆
.所以椭圆 的方程为
的方程为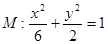 .…………………4分
.…………………4分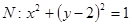 的圆心为
的圆心为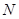 ,
,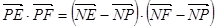 ……………………6分
……………………6分
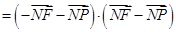 ……K…………………………7分
……K…………………………7分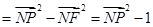 .………………………………………8分
.………………………………………8分 的最大值转化为求
的最大值转化为求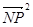 的最大值.………………………9分
的最大值.………………………9分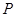 是椭圆
是椭圆 上的任意一点,设
上的任意一点,设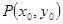 ,……………………………10分
,……………………………10分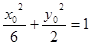 ,即
,即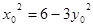 .…………………………11分
.…………………………11分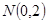 ,所以
,所以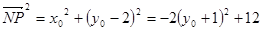 .……………12分
.……………12分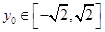 ,所以当
,所以当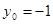 时,
时,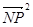 取得最大值12.……………13分
取得最大值12.……………13分 的最大值为11.……………………………14分
的最大值为11.……………………………14分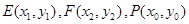 ,
, 的中点坐标为
的中点坐标为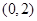 ,所以
,所以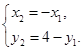 …………………………6分
…………………………6分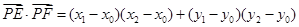 ……………………7分
……………………7分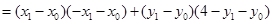
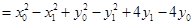
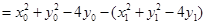 .……………………………9分
.……………………………9分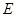 在圆
在圆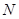 上,所以
上,所以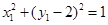 ,即
,即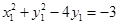 .…………10分
.…………10分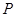 在椭圆
在椭圆 上,所以
上,所以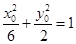 ,即
,即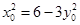 .………………11分
.………………11分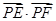
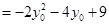
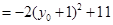 .……………………………12分
.……………………………12分 ,所以当
,所以当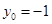 时,
时,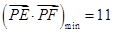 .…………………14分
.…………………14分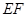 的斜率存在,设
的斜率存在,设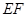 的方程为
的方程为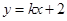 ,……………6分
,……………6分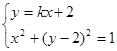 ,解得
,解得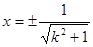 .………………………7分
.………………………7分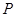 是椭圆
是椭圆 上的任一点,设点
上的任一点,设点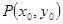 ,
,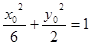 ,即
,即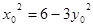 .…………………8分
.…………………8分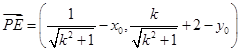 ………9分
………9分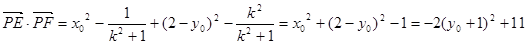 .
.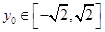 ,所以当
,所以当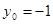 时,
时, 取得最大值11.……………11分
取得最大值11.……………11分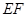 的斜率不存在,此时
的斜率不存在,此时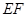 的方程为
的方程为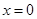 ,
, 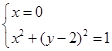 ,解得
,解得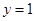 或
或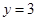 .
.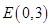 ,
,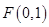 .……………………5u…………………12分
.……………………5u…………………12分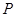 是椭圆
是椭圆 上的任一点,设点
上的任一点,设点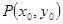 ,
,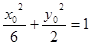 ,即
,即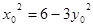 .
.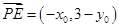 ,
,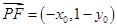 .
.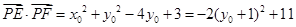 .
. 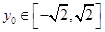 ,所以当
,所以当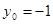 时,
时, 取得最大值11.………13分
取得最大值11.………13分 的最大值为11.…………………………………14分
的最大值为11.…………………………………14分

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com