
【题目】根据要求求值:
(1)用辗转相除法求123和48的最大公约数.
(2)用更相减损术求80和36的最大公约数.
(3)把89化为二进制数.
【答案】
(1)解:辗转相除法求最大公约数的过程如下:
123=2×48+27,48=1×27+21,27=1×21+6,21=3×6+3,6=2×3+0,
最后6能被3整除,得123和48的最大公约数为3
(2)解:我们将80作为大数,36作为小数,因为80和36都是偶数,要除公因数2.
80÷2=40,36÷2=18.40和18都是偶数,要除公因数2.40÷2=20,18÷2=9.
求20与9的最大公约数,20﹣9=11,11﹣9=2,9﹣2=7,7﹣2=5,5﹣2=3,3﹣2=1,
2﹣1=1,可得80和36的最大公约数为22×1=4.
(3)解:如图所示,可得:89(10)=1 011 001(2).
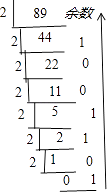
【解析】(1)利用辗转相除法即可得出;(2)我们将80作为大数,36作为小数,因为80和36都是偶数,要除公因数2.依此类推可得:80÷4=20,36÷4=9.利用更相减损术求20与9的最大公约数,即可得出.(3)如图所示,即可得出.
【考点精析】本题主要考查了进位制的相关知识点,需要掌握进位制是一种记数方式,用有限的数字在不同的位置表示不同的数值才能正确解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】路灯距地面8 m,一个身高为1.6 m的人以84 m/min的速度在地面上从路灯在地面上射影点C沿某直线离开路灯.
(1)求身影的长度y与人距路灯的距离x之间的关系式;
(2)求人离开路灯的第一个10 s内身影的平均变化率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直角梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,如图1所示,将
,如图1所示,将![]() 沿
沿![]() 折起到
折起到![]() 的位置,如图2所示.
的位置,如图2所示.
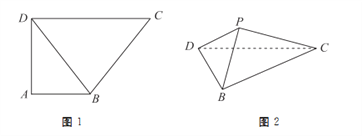
(1)当平面![]() 平面
平面![]() 时,求三棱锥
时,求三棱锥![]() 的体积;
的体积;
(2)在图2中, ![]() 为
为![]() 的中点,若线段
的中点,若线段![]() ,且
,且![]() 平面
平面![]() ,求线段
,求线段![]() 的长;
的长;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,F1,F2分别是椭圆C:![]() 的左、右焦点,A是椭圆C的顶点,B是直线AF2与椭圆C的另一个交点,∠F1AF2=60°.
的左、右焦点,A是椭圆C的顶点,B是直线AF2与椭圆C的另一个交点,∠F1AF2=60°.
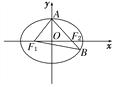
(1)求椭圆C的离心率;
(2)已知△AF1B的面积为40![]() ,求a,b的值.
,求a,b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(cos
=(cos ![]() x,sin
x,sin ![]() x),
x), ![]() =(cos
=(cos ![]() x,﹣sin
x,﹣sin ![]() x),且x∈[0,
x),且x∈[0, ![]() ].求:
].求:
(1)![]() 及
及 ![]() ;
;![]()
(2)若f(x)= ![]() ﹣2λ
﹣2λ ![]() 的最小值是﹣
的最小值是﹣ ![]() ,求λ的值.
,求λ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从甲、乙两名学生中选拔一人参加射箭比赛,为此需要对他们的射箭水平进行测试.现这两名学生在相同条件下各射箭10次,命中的环数如表:
甲 | 8 | 9 | 7 | 9 | 7 | 6 | 10 | 10 | 8 | 6 |
乙 | 10 | 9 | 8 | 6 | 8 | 7 | 9 | 7 | 8 | 8 |
(1)计算甲、乙两人射箭命中环数的平均数和标准差;
(2)比较两个人的成绩,然后决定选择哪名学生参加射箭比赛.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设{an}是由正数组成的等比数列,公比q=2,且a1a2a3…a30=230 , 那么a3a6a9…a30等于( )
A.210
B.220
C.216
D.215
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形![]() 为菱形,
为菱形, ![]() ,
, ![]() 与
与![]() 相交于点
相交于点![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() 为
为![]() 中点.
中点.
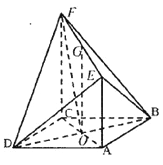
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的正弦值;
的正弦值;
(Ⅲ)当直线![]() 与平面
与平面![]() 所成角为
所成角为![]() 时,求异面直线
时,求异面直线![]() 与
与![]() 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com