练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    等差数列{an}的前n项和为Sn，已知S10＝0，S15＝25，则nSn的最小值为________．


    －49


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知向量a与b的夹角为60°，且a＝(－2，－6)，|b|＝，则a·b＝________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


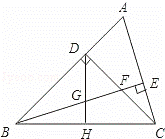
    已知：如图，△ABC中，∠ABC=45°，CD⊥AB于D，BE平分∠ABC，且BE⊥AC于E，与CD相交于点F，H是BC边的中点，连接DH与BE相交于点G．

    （1）求证：BF=AC；

    （2）求证：CE=BF；

    （3）CE与BG的大小关系如何？试证明你的结论．

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知等差数列{an}的前n项和为Sn，a4＝15，S5＝55，则数列{an}的公差是(　　)

    A.                                    B．4

    C．－4                                  D．－3

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在等差数列{an}中，an>0，且a1＋a2＋…＋a10＝30，则a5·a6的最大值为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知等比数列{an}的前n项积记为Πn，若a3a4a8＝8，则Π9＝(　　)

    A．512                                  B．256

    C．81                                   D．16

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知在正项数列{an}中，a1＝2，点An(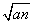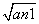，)在双曲线y2－x2＝1上，数列{bn}中，点(bn，Tn)在直线y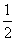＝－x＋1上，其中Tn是数列{bn}的前n项和．

    (1)求数列{an}的通项公式；

    (2)求证：数列{bn}是等比数列；

    (3)若cn＝an·bn，求证：cn＋1<cn.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知数列{an}中，a1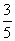＝，an＝2－(n≥2，n∈N*)，数列{bn}满足bn＝(n∈N*)．

    (1)证明：数列{bn}是等差数列；

    (2)若Sn＝(a1－1)·(a2－1)＋(a2－1)·(a3－1)＋…＋(an－1)·(an＋1－1)，是否存在a，b∈Z，使得a≤Sn≤b恒成立？若存在，求出a的最大值与b的最小值；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设非空集合M同时满足下列两个条件：

    ①M⊆{1,2,3，…，n－1}；②若a∈M，则n－a∈M(n≥2，n∈N*)，则下列结论正确的是(　　)

    A．若n为偶数，则集合M的个数为2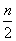个

    B．若n为偶数，则集合M的个数为2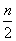－1个

    C．若n为奇数，则集合M的个数为2个

    D．若n为奇数，则集合M的个数为2个

    查看答案和解析>>

    同步练习册答案