
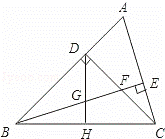
已知:如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连接DH与BE相交于点G.
(1)求证:BF=AC;
(2)求证:CE= BF;
BF;
(3)CE与BG的大小关系如何?试证明你的结论.
(1)证明:∵CD⊥AB,∠ABC=45°,
∴△BCD是等腰直角三角形.
∴BD=CD.
∵∠DBF=90°﹣∠BFD,∠DCA=90°﹣∠EFC,且∠BFD=∠EFC,
∴∠DBF=∠DCA.
在Rt△DFB和Rt△DAC中,
∵
∴Rt△DFB≌Rt△DAC(ASA).
∴BF=AC;
(2)证明:∵BE平分∠ABC,
∴∠ABE=∠CBE.
在Rt△BEA和Rt△BEC中
 ,
,
∴Rt△BEA≌Rt△BEC(ASA).
∴CE=AE= AC.
AC.
又由(1),知BF=AC,
∴CE= AC=
AC= BF;
BF;
(3)证明:∠ABC=45°,CD垂直AB于D,则CD=BD.
H为BC中点,则DH⊥BC(等腰三角形“三线合一”)
连接CG,则BG=CG,∠GCB=∠GBC= ∠ABC=
∠ABC= ×45°=22.5°,∠EGC=45°.
×45°=22.5°,∠EGC=45°.
又∵BE垂直AC,故∠EGC=∠ECG=45°,CE=GE.
∵△GEC是直角三角形,
∴CE2+GE2=CG2,
∵DH垂直平分BC,
∴BG=CG,
∴CE2+GE2=CG2=BG2;即2CE2=BG2,BG= CE,
CE,
∴BG>CE.



 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:
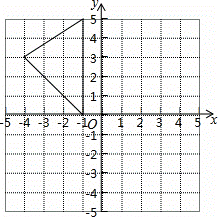
如图,在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
(1)求出△ABC的面积;
(2)在图中作出△ABC关于y轴的对称图形△A1B1C1;
(3)写出点A1,B1,C1的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
设数列{an}的前n项和为Sn,已知a1=a,an+1=Sn+3n,n∈N*.
(1)记bn=Sn-3n,求数列{bn}的通项公式;
(2)若an+1≥an,n∈N*,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com