
已知数列{an}中,a1=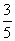 ,an=2-
,an=2- (n≥2,n∈N*),数列{bn}满足bn=
(n≥2,n∈N*),数列{bn}满足bn= (n∈N*).
(n∈N*).
(1)证明:数列{bn}是等差数列;
(2)若Sn=(a1-1)·(a2-1)+(a2-1)·(a3-1)+…+(an-1)·(an+1-1),是否存在a,b∈Z,使得a≤Sn≤b恒成立?若存在,求出a的最大值与b的最小值;若不存在,请说明理由.
 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:高中数学 来源: 题型:
植树节某班20名同学在一段直线公路一侧植树,每人植一棵,相邻两棵树相距10米.开始时需将树苗集中放置在某一树坑旁边.使每位同学从各自树坑出发前来领取树苗往返所走的路程总和最小,这个最小值为________米.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知数列{an}的通项公式为an=n2cosnπ(n∈N*),Sn为它的前n项和,则 等于( )
等于( )
A.1 005 B.1 006
C.2 011 D.2 012
查看答案和解析>>
科目:高中数学 来源: 题型:
已知q和n均为给定的大于1的自然数.设集合M={0,1,2,…,q-1},集合A={x|x=x1+x2q+…+xnqn-1,xi∈M,i=1,2,…,n}.
(1)当q=2,n=3时,用列举法表示集合A;
(2)设s,t∈A,s=a1+a2q+…+anqn-1,t=b1+b2q+…+bnqn-1,其中ai,bi∈M,i=1,2,…,n.证明:若an<bn,则s<t.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com