
已知q和n均为给定的大于1的自然数.设集合M={0,1,2,…,q-1},集合A={x|x=x1+x2q+…+xnqn-1,xi∈M,i=1,2,…,n}.
(1)当q=2,n=3时,用列举法表示集合A;
(2)设s,t∈A,s=a1+a2q+…+anqn-1,t=b1+b2q+…+bnqn-1,其中ai,bi∈M,i=1,2,…,n.证明:若an<bn,则s<t.
科目:高中数学 来源: 题型:
已知数列{an}中,a1=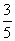 ,an=2-
,an=2- (n≥2,n∈N*),数列{bn}满足bn=
(n≥2,n∈N*),数列{bn}满足bn= (n∈N*).
(n∈N*).
(1)证明:数列{bn}是等差数列;
(2)若Sn=(a1-1)·(a2-1)+(a2-1)·(a3-1)+…+(an-1)·(an+1-1),是否存在a,b∈Z,使得a≤Sn≤b恒成立?若存在,求出a的最大值与b的最小值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
要证a2+b2-1-a2b2≤0,只要证明( )
A.2ab-1-a2b2≤0
B.a2+b2-1-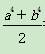 ≤0
≤0
C. -1-a2b2≤0
-1-a2b2≤0
D.(a2-1)(b2-1)≥0
查看答案和解析>>
科目:高中数学 来源: 题型:
已知点An(n,an)为函数y= 的图象上的点,Bn(n,bn)为函数y=x图象上的点,其中n∈N*,设cn=an-bn,则cn与cn+1的大小关系为__________.
的图象上的点,Bn(n,bn)为函数y=x图象上的点,其中n∈N*,设cn=an-bn,则cn与cn+1的大小关系为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
在平面几何中有如下结论:正三角形ABC的内切圆面积为S1,外接圆面积为S2,则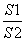 =
=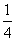 ,推广到空间可以得到类似结论:已知正四面体P—ABC的内切球体积为V1,外接球体积为V2,则
,推广到空间可以得到类似结论:已知正四面体P—ABC的内切球体积为V1,外接球体积为V2,则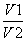 =( )
=( )
A.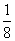 B.
B.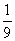
C. D.
D.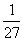
查看答案和解析>>
科目:高中数学 来源: 题型:
设非空集合M同时满足下列两个条件:
①M⊆{1,2,3,…,n-1};②若a∈M,则n-a∈M(n≥2,n∈N*),则下列结论正确的是( )
A.若n为偶数,则集合M的个数为2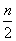 个
个
B.若n为偶数,则集合M的个数为2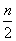 -1个
-1个
C.若n为奇数,则集合M的个数为2 个
个
D.若n为奇数,则集合M的个数为2 个
个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com