考点:直线与平面平行的判定,几何概型
专题:综合题,空间位置关系与距离,概率与统计
分析:(Ⅰ)证明AD∥平面EFGH,只需证明AD∥EH;
(Ⅱ)根据几何槪型的概率公式,结合基本不等式求出取自于几何体A1ABFE-D1DCGH内的概率为p的最小值,即可求出概率.
解答:
(Ⅰ)证明:∵AD∥A
1D
1,EH∥A
1D
1,
∴AD∥EH,
∵AD?平面EFGH,EH?平面EFGH
∴AD∥平面EFGH;
(Ⅱ)解:根据几何槪型的概率公式可知,点取自于几何体A
1ABFE-D
1DCGH内的概率为P=
| VA1ABFE-D1DCGH |
| VABCD-A1B1C1D1 |
,
∴若p最小,则只需几何体A
1ABFE-D
1DCGH的体积最小,即五边形A
1ABFE的面积最小,等价为三角形EFB
1的面积最大,
∵EF=a,
∴
B1E2+B1F2=a
2,
则S
△B1EF=
B1E•B1F≤
(B
1E
2+B
1F
2)=
,当且仅当B
1F=B
1E时取等号,
此时五边形A
1ABFE的面积最小为2a
2-
=
,
则取自于几何体A
1ABFE-D
1DCGH内的概率为P=
| VA1ABFE-D1DCGH |
| VABCD-A1B1C1D1 |
=
.
点评:本题主要考查线面平行,考查几何槪型的概率计算,根据体积槪型结合基本不等式求出最值是解决本题的关键.

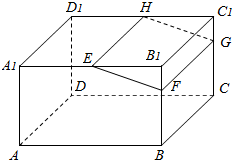 如图,在长方体ABCD-A1B1C1D1中,E、H分别是棱A1B1,D1C1上的点(点E与B1不重合),且EH∥A1D1,过EH的平面与棱BB1,CC1相交,交点分别为F,G
如图,在长方体ABCD-A1B1C1D1中,E、H分别是棱A1B1,D1C1上的点(点E与B1不重合),且EH∥A1D1,过EH的平面与棱BB1,CC1相交,交点分别为F,G

 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案 根据如图所示的程序框图,将输出的x、y值依次分别记为x1,x2,…,xn,…,x2007;y1,y2,…,yn…,y2007;
根据如图所示的程序框图,将输出的x、y值依次分别记为x1,x2,…,xn,…,x2007;y1,y2,…,yn…,y2007;
