
| A. | 24 | B. | 18 | C. | 12 | D. | 6 |
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $A_5^5A_4^2$ | B. | $A_5^5A_5^2$ | C. | $A_5^5A_6^2$ | D. | $A_7^7-4A_6^6$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
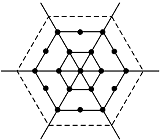 如图所示是一个有n层(n≥2,n∈N*)的六边形点阵,它的中心是一个点,算作第1层,第2层每边有2个点,第3层每边有3个点,…,第n层每边有n个点,则这个点阵共有( )个点.
如图所示是一个有n层(n≥2,n∈N*)的六边形点阵,它的中心是一个点,算作第1层,第2层每边有2个点,第3层每边有3个点,…,第n层每边有n个点,则这个点阵共有( )个点.| A. | n2 | B. | n2+n | C. | 3n2-3n+1 | D. | 3n2-3n |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
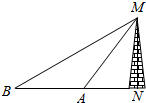 如图,要测量电视塔的高度,测量者在点A处测得对电视塔的仰角为60°,然后测量者后退200米到点B,测得对电视塔的仰角为30°,则电视塔的高度为( )
如图,要测量电视塔的高度,测量者在点A处测得对电视塔的仰角为60°,然后测量者后退200米到点B,测得对电视塔的仰角为30°,则电视塔的高度为( )| A. | 100$\sqrt{2}$m | B. | 100$\sqrt{3}$m | C. | 100m | D. | 200m |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com