
分析 (1)求导数f′(x)=$\frac{{x}^{2}-a}{{x}^{2}}$,根据导数符号即可得出f(x)在区间(0,$\sqrt{a}$]上为减函数,在[$\sqrt{a}$,+∞)上为增函数;
(2)根据上面导数符号的判断过程即知x=$\sqrt{a}$时,f(x)取最小值,求出该值即可.
解答 解:(1)证明:f′(x)=$\frac{{x}^{2}-a}{{x}^{2}}$;
∴x∈(0,$\sqrt{a}$]时,f′(x)≤0,x∈[$\sqrt{a}$,+∞)时,f′(x)≥0;
∴f(x)在区间$(0,\sqrt{2}]$上为减函数,在$[\sqrt{a},+∞)$上为增函数;
(2)由(1)知,x=$\sqrt{a}$时,f(x)取最小值$2\sqrt{a}$.
点评 考查根据导数符号证明函数在一区间上的单调性的方法,以及根据导数求函数最值的方法及过程,要正确求导.


科目:高中数学 来源: 题型:解答题
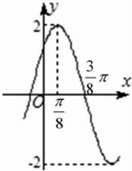 函数f(x)=2sin(ωx+φ),(ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示,
函数f(x)=2sin(ωx+φ),(ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示,查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com