
分析 (1)利用导数的几何意义求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)(i)分类讨论,利用函数的单调性,即可求实数t的最大值;
(ii)当x>1时整理得$2lnx<\frac{{{x^2}-1}}{x}=x-\frac{1}{x}$,令$x=\frac{k}{k-1}$,则$2ln\frac{k}{k-1}<\frac{k}{k-1}-\frac{k-1}{k}=\frac{1}{k}+\frac{1}{k-1}$,即可证明不等式.
解答 解:(1)由题意x∈(0,+∞)且$f'(x)=\frac{{\frac{1}{x}(x+1)-lnx}}{{{{(x+1)}^2}}}=\frac{x+1-xlnx}{{x{{(x+1)}^2}}}$,∴$f'(1)=\frac{2-0}{4}=\frac{1}{2}$,
又$f(1)=\frac{0}{2}=0$,∴f(x)在点(1,f(1))处的切线方程为$y-0=\frac{1}{2}(x-1)$,即x-2y-1=0.
(2)(i)由题意知$\frac{lnx}{x+1}-\frac{lnx}{x-1}-\frac{t}{x}>0$,
设$g(x)=\frac{lnx}{x+1}-\frac{lnx}{x-1}-\frac{t}{x}$,则$g'(x)=\frac{(x-1)-(x+1)}{{{x^2}-1}}lnx-\frac{t}{x}$=$\frac{1}{{1-{x^2}}}[2lnx+\frac{{t({x^2}-1)}}{x}]$,设$h(x)=2lnx+\frac{{t({x^2}-1)}}{x}$,则$h'(x)=\frac{2}{x}+t(1+\frac{1}{x^2})=\frac{{t{x^2}+2x+t}}{x^2}$,
当t≥0时,∵x>0,∴h'(x)>0,∴h(x)在(0,+∞)上单调递增,
又h(1)=0,∴x∈(0,1)时,h(x)<0,
又$\frac{1}{{1-{x^2}}}>0$,∴g(x)<0不符合题意.
当t<0时,设ϕ(x)=tx2+2x+t,
①若△=4-4t2≤0即t≤1时,ϕ(x)≤0恒成立,即h'(x)≤0在(0,+∞)恒成立,
∴h(x)在(0,+∞)上单调递减,
又h(1)=0,∴x∈(0,1)时,h(x)>0,$\frac{1}{{1-{x^2}}}>0$,g(x)>0,x∈(1,+∞)时,h(x)<0,$\frac{1}{{1-{x^2}}}<0$,g(x)>0,符合题意.
②若△=4-4t2>0即-1<t<0时,ϕ(x)的对称轴$x=-\frac{1}{t}>1$,∴ϕ(x)在$(1,-\frac{1}{t})$上单调递增,
∴$x∈(1,-\frac{1}{t})$时,ϕ(x)>ϕ(1)=2+2t>0,∴h'(x)>0,∴h(x)在$(1,-\frac{1}{t})$上单调递增,
∴h(x)>h(1)=0,而$\frac{1}{{1-{x^2}}}<0$,∴g(x)<0,不符合题意.
综上所述t≤-1,∴t的最大值为-1.
(ii)由(i)知t=-1时,$\frac{lnx}{x+1}-\frac{lnx}{x-1}+\frac{1}{x}>0$,
当x>1时整理得$2lnx<\frac{{{x^2}-1}}{x}=x-\frac{1}{x}$,令$x=\frac{k}{k-1}$,则$2ln\frac{k}{k-1}<\frac{k}{k-1}-\frac{k-1}{k}=\frac{1}{k}+\frac{1}{k-1}$,
∴$2[ln\frac{2}{1}+ln\frac{3}{2}+…+ln\frac{n}{n-1}]<1+\frac{1}{2}+\frac{1}{2}+\frac{1}{3}+…+\frac{1}{n-2}+\frac{1}{n-1}+\frac{1}{n-1}+\frac{1}{n}$,
∴$2lnn<1+2[\frac{1}{2}+\frac{1}{3}+…+\frac{1}{n-1}]+\frac{1}{n}$,
∴$lnn<1+\frac{1}{2}+\frac{1}{3}+…+\frac{1}{n}-\frac{1}{2}-\frac{1}{2n}$,即$lnn<\sum_{i=1}^n{\frac{1}{i}}-\frac{1}{2}-\frac{1}{2n}$.
点评 本题考查导数知识的综合运用,考查导数的几何意义,考查不等式的证明,体现分类讨论的数学思想,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 恒为正 | B. | 等于零 | C. | 恒为负 | D. | 不小于零 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
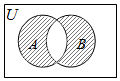
| A. | {1} | B. | {1,2,3,5} | C. | { 2,3,5} | D. | {4} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com