
分析 (Ⅰ)先求函数的定义域,再求导,分类讨论,根据导数和函数的单调性即可求函数的单调区间;
(Ⅱ)不妨设x1>x2,转化为(x1)-4x1≥f(x2)-4x2恒成立,构造函数,利用导数和函数的最值的关系即可求出a的取值范围.
解答 解:(Ⅰ)∵f(x)的定义域为(0,+∞)
∴$f'(x)=\frac{a+1}{x}+2x=\frac{{2{x^2}+a+1}}{x}$,
当a+1≥0时,f′(x)>0恒成立,
∴当a≥-1时,y=f(x)在区间(0,+∞)单调递增,
当a+1<0时,若x>$\sqrt{-\frac{a+1}{2}}$,f′(x)>0,
若0<x<$\sqrt{-\frac{a+1}{2}}$,f′(x)<0,
∴当a<-1时,函数y=f(x)在区间(0,$\sqrt{-\frac{a+1}{2}}$)上单调递减,在区间($\sqrt{-\frac{a+1}{2}}$,+∞)上单调递增,
(Ⅱ)不妨设x1>x2,
又∵a≥0,
∴y=f(x)在区间(0,+∞)上单调递增|f(x1)-f(x2)|≥4|x1-x2|恒成立,等价于f(x1)-f(x2)≥4x1-4x2恒成立,
即就是f(x1)-4x1≥f(x2)-4x2恒成立
令g(x)=f(x)-4x,x∈(0,+∞),则y=g(x)为单调递增函数
即就是g'(x)≥0恒成立,
∵$g'(x)=\frac{{2{x^2}-4x+a+1}}{x}≥0$
令h(x)=2x2-4x+a+1,x∈(0,+∞),
∵h(x)min=h(1)=a-1,
∴a≥1,
故a的取值范围为[1,+∞)
点评 该题考查利用导数研究函数的单调性、最值,考查函数恒成立问题,考查转化思想,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{{\sqrt{21}}}$ | B. | $\frac{3}{{\sqrt{21}}}$ | C. | $\frac{4}{{\sqrt{21}}}$ | D. | $\frac{5}{{\sqrt{21}}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3∈A | B. | A=B | C. | A∩B=A | D. | A∪B=Z |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
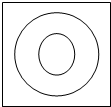 如图,在墙上挂着一块边长为16cm的正方形木板,上面画了大、小两个同心圆,半径分别为2cm,6cm,某人站在3m之外向此板投镖,设投镖击中线上或没有投中木板时都不算(可重投),问:
如图,在墙上挂着一块边长为16cm的正方形木板,上面画了大、小两个同心圆,半径分别为2cm,6cm,某人站在3m之外向此板投镖,设投镖击中线上或没有投中木板时都不算(可重投),问:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com