
分析 (I)利用余弦定理即可得出.
(II)在直角坐标系中,圆心$C(\frac{{\sqrt{2}}}{2},\frac{{\sqrt{2}}}{2})$,可得圆C的方程,设Q(x,y),则P(2x,2y),代入圆的方程即可得出.
解答 解:(Ⅰ)设点P的极坐标为(ρ,θ),
由余弦定理得${1^2}={ρ^2}+{1^2}-2ρcos(θ-\frac{π}{4})$,
即${ρ^2}=2ρcos(θ-\frac{π}{4})$,∴圆C的极坐标方程为$ρ=2cos(θ-\frac{π}{4})$.
(Ⅱ)在直角坐标系中,圆心$C(\frac{{\sqrt{2}}}{2},\frac{{\sqrt{2}}}{2})$,
圆C的方程为${(x-\frac{{\sqrt{2}}}{2})^2}+{(y-\frac{{\sqrt{2}}}{2})^2}=1$.
设Q(x,y),则P(2x,2y),
由点P在圆C上得${(2x-\frac{{\sqrt{2}}}{2})^2}+{(2y-\frac{{\sqrt{2}}}{2})^2}=1$,即${(x-\frac{{\sqrt{2}}}{4})^2}+{(y-\frac{{\sqrt{2}}}{4})^2}=\frac{1}{4}$,
故点Q轨迹的直角坐标方程为${(x-\frac{{\sqrt{2}}}{4})^2}+{(y-\frac{{\sqrt{2}}}{4})^2}=\frac{1}{4}$.
点评 本题考查了极坐标方程化为直角坐标方程、圆的标准方程、余弦定理,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
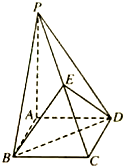 如图,四边形ABCD为菱形,∠ABC=60°,PA⊥平面ABCD,E为PC的中点.
如图,四边形ABCD为菱形,∠ABC=60°,PA⊥平面ABCD,E为PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -6-3△t | B. | -6+3△t | C. | 8-3△t | D. | 8+3△t |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com