
分析 利用三角函数的图象与性质、诱导公式、数列的递推关系可得an+1-an=nπ,再利用“累加求和”方法、等差数列的求和公式即可得出.
解答 解:∵a1=0,当n=1时,f1(x)=|sin(x-a1)|=|sinx|,x∈[0,a2],
又∵对任意的b∈[0,1),f1(x)=b总有两个不同的根,∴a2=π,
∴f1(x)=sinx,x∈[0,π],a2=π,
又f2(x)=|sin$\frac{1}{2}$(x-a2)|=|sin$\frac{1}{2}$(x-π)|=|cos$\frac{x}{2}$|,x∈[π,a3],
∵对任意的b∈[0,1),f1(x)=b总有两个不同的根,∴a3=3π,
又f3(x)=|sin$\frac{1}{3}$(x-a3)|=|sin$\frac{1}{3}$(x-3π)|=|sin$\frac{1}{3}$π|,x∈[3π,a4],
∵对任意的b∈[0,1),f1(x)=b总有两个不同的根,∴a4=6π,
由此可得an+1-an=nπ,
∴an=a1+(a2-a1)+…+(an-an-1)=0+π+…+(n-1)π=$\frac{n(n-1)}{2}$π,an=$\frac{n(n-1)}{2}$π.
故答案为:$\frac{n(n-1)}{2}$π.
点评 本题考查了三角函数的图象与性质、诱导公式、数列的递推关系、“累加求和”方法、等差数列的求和公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | -π+arcsin$\frac{\sqrt{2}}{4}$ | B. | -π-arcsin$\frac{\sqrt{2}}{4}$ | C. | -$\frac{3π}{2}$+arcsin$\frac{\sqrt{2}}{4}$ | D. | -2π+arcsin$\frac{\sqrt{2}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x+y-π=0 | B. | 2x+2y-π=0 | C. | 2x-π2y-2π=0 | D. | 2x+π2y-2π=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
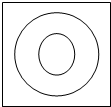 如图,在墙上挂着一块边长为16cm的正方形木板,上面画了大、小两个同心圆,半径分别为2cm,6cm,某人站在3m之外向此板投镖,设投镖击中线上或没有投中木板时都不算(可重投),问:
如图,在墙上挂着一块边长为16cm的正方形木板,上面画了大、小两个同心圆,半径分别为2cm,6cm,某人站在3m之外向此板投镖,设投镖击中线上或没有投中木板时都不算(可重投),问:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | S12 | B. | S7 | C. | S6 | D. | S1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com