
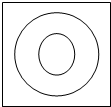
 如图,在墙上挂着一块边长为16cm的正方形木板,上面画了大、小两个同心圆,半径分别为2cm,6cm,某人站在3m之外向此板投镖,设投镖击中线上或没有投中木板时都不算(可重投),问:
如图,在墙上挂着一块边长为16cm的正方形木板,上面画了大、小两个同心圆,半径分别为2cm,6cm,某人站在3m之外向此板投镖,设投镖击中线上或没有投中木板时都不算(可重投),问:分析 本题考查的知识点是几何概型的意义,关键是要找出符合题意部分的面积,及正方形木板的面积,并将其代入几何概型计算公式中进行求解.
(1)求出正方形的面积,求出大圆的面积,利用几何概型的概率公式求出投中大圆内的概率.
(2)求出正方形的面积,求出小圆与大圆形成的圆环的面积,利用几何概型的概率公式求出投中小圆与大圆形成的圆环的概率.
解答 解:整个正方形木板的面积,即基本事件所占的区域的总面积为μΩ=16×16=256cm2,
记“投中大圆内”为事件A,“投中小圆与大圆形成的圆环”为事件B,
则事件A所占区域面积为μA=π×62=36πcm2;
事件B所占区域面积为μB=π×62-π×22=32πcm2;
由几何概型的概率公式,
得(1)投中大圆内的概率是$\frac{36π}{256}$=$\frac{9π}{64}$;
(2)投中小圆与大圆形成的圆环的概率是$\frac{32π}{256}$=$\frac{π}{8}$.
点评 本题考查圆的面积公式、几何概型的概率公式、对立事件的概率公式等.属于基础题.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源: 题型:解答题
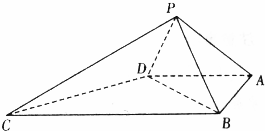 如图,四棱锥P-ABCD中,∠ABC=∠BAD=90°,BC=2AD=2,△PAB与△PAD都是等边三角形.
如图,四棱锥P-ABCD中,∠ABC=∠BAD=90°,BC=2AD=2,△PAB与△PAD都是等边三角形.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -6-3△t | B. | -6+3△t | C. | 8-3△t | D. | 8+3△t |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com