
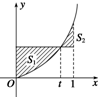
 在区间[0,1]上给定曲线y=x2,如图所示,0<t<1,S1,S2是t的函数,则函数g(t)=S1+S2的单调递增区间为($\frac{1}{2}$,1).
在区间[0,1]上给定曲线y=x2,如图所示,0<t<1,S1,S2是t的函数,则函数g(t)=S1+S2的单调递增区间为($\frac{1}{2}$,1). 分析 首先利用定积分分别求出S1,S2,得到函数g(t),然后分析其单调性.
解答 解:由题意S1=${∫}_{0}^{t}{(t}^{2}-{x}^{2})dx$=(t2x-$\frac{1}{3}{x}^{3}$)|${\;}_{0}^{t}$=$\frac{2}{3}{t}^{3}$,
S2=${∫}_{t}^{1}({x}^{2}-{t}^{2})dx$=($\frac{1}{3}{x}^{3}-{t}^{2}x$)|${\;}_{t}^{1}$=$\frac{1}{3}-{t}^{2}+\frac{2}{3}{t}^{3}$,
所以g(t)=S1+S2=$\frac{4}{3}{t}^{3}-{t}^{2}+\frac{1}{3}$,g'(t)=4t2-2t=2t(2t-1),令g'(t)>0解得t>$\frac{1}{2}$或t<0,又0<t<1,
所以函数g(t)=S1+S2的单调递增区间为($\frac{1}{2}$,1);
故答案为:($\frac{1}{2}$,1).
点评 本题考查了利用定积分求曲边梯形的面积以及利用导数求函数的单调区间;属于经常考查的题型.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案科目:高中数学 来源: 题型:选择题
| A. | {1,3} | B. | [1,5) | C. | {1,3,5} | D. | ∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 存在四边相等的四边形不是正方形 | |
| B. | 设x,y∈R,则“(x-y)•x2<0”是“x<y”的必要而不充分条件 | |
| C. | 若x,y∈R,且x+y>2,则x,y至少有一个大于1 | |
| D. | 命题:?n∈N,2n>1000的否定是:?n∈N,2n≤1000 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5π}{56}$ | B. | $\frac{5}{56}$ | C. | $\frac{5π}{28}$ | D. | $\frac{5}{28}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com