
【题目】随着我国互联网信息技术的发展,网络购物已经成为许多人消费的一种重要方式,某市为了了解本市市民的网络购物情况,特委托一家网络公示进行了网络问卷调查,并从参与调查的10000名网民中随机抽取了200人进行抽样分析,得到了下表所示数据:
经常进行网络购物 | 偶尔或从不进行网络购物 | 合计 | |
男性 | 50 | 50 | 100 |
女性 | 60 | 40 | 100 |
合计 | 110 | 90 | 200 |
(1)依据上述数据,能否在犯错误的概率不超过![]() 的前提下认为该市市民进行网络购物的情况与性别有关?
的前提下认为该市市民进行网络购物的情况与性别有关?
(2)现从所抽取的女性网民中利用分层抽样的方法再抽取![]() 人,从这
人,从这![]() 人中随机选出
人中随机选出![]() 人赠送网络优惠券,求出选出的
人赠送网络优惠券,求出选出的![]() 人中至少有两人是经常进行网络购物的概率;
人中至少有两人是经常进行网络购物的概率;
(3)将频率视为概率,从该市所有的参与调查的网民中随机抽取![]() 人赠送礼物,记经常进行网络购物的人数为
人赠送礼物,记经常进行网络购物的人数为![]() ,求
,求![]() 的期望和方差.
的期望和方差.
附:![]() ,其中
,其中![]()

【答案】(1)见解析;(2)见解析
【解析】试题分析:(1)由列联表中的数据计算![]() 的观测值,对照临界值得出结论;(2)利用分层抽样原理求出所抽取的5名女网民中经常进行网购和偶尔或不进行网购的人数,计算所求的概率值;(3)由列联表中数据计算经常进行网购的频率,将频率视为概率知随机变量
的观测值,对照临界值得出结论;(2)利用分层抽样原理求出所抽取的5名女网民中经常进行网购和偶尔或不进行网购的人数,计算所求的概率值;(3)由列联表中数据计算经常进行网购的频率,将频率视为概率知随机变量![]() 服从
服从![]() 次独立重复实验的概率模型,计算数学期望与方差的大小.
次独立重复实验的概率模型,计算数学期望与方差的大小.
试题解析:(1)由列联表数据计算![]() .
.
所以,不能再犯错误的概率不超过![]() 的前提下认为该市市民网购情况与性别有关.
的前提下认为该市市民网购情况与性别有关.
(2)由题意,抽取的5名女性网民中,经常进行网购的有![]() 人,偶尔或从不进行网购的有
人,偶尔或从不进行网购的有![]() 人,故从这5人中选出3人至少有2人经常进行网购的概率是
人,故从这5人中选出3人至少有2人经常进行网购的概率是![]() .
.
(3)由列联表可知,经常进行网购的频率为![]() .
.
由题意,从该市市民中任意抽取1人恰好是经常进行网购的概率是![]() .
.
由于该市市民数量很大,故可以认为![]() .
.
所以,![]() ,
,![]() .
.


科目:高中数学 来源: 题型:
【题目】为了纪念五四运动100周年和建团97周年,某校团委开展“青春心向党,建功新时代”知识问答竞赛.在小组赛中,甲乙丙3人进行擂台赛,每局2人进行比赛,另1人当裁判,每一局的输方担任下局的裁判,由原来裁判向胜者挑战,甲乙丙3人实力相当.
(1)若第1局是由甲担任裁判,求第4局仍是甲担任裁判的概率;
(2)甲乙丙3人进行的擂台赛结束后,经统计,甲共参赛了6局,乙共参赛了5局而丙共担任了2局裁判.则甲乙丙3人进行的擂台赛共进行了多少局?若从小组赛中,甲乙丙比赛的所有场次中任取2场,则均是由甲担任裁判的概率是多少.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高老师需要用“五点法”画函数![]() 在一个周期内的图像,此时的高老师已经将部分数据填入表格,如下表:
在一个周期内的图像,此时的高老师已经将部分数据填入表格,如下表:
|
|
|
0 | a=? | 0 |
|
| 5 |
|
| 0 |
|
| -5 |
| b=? | 0 |
(1)请同学们帮助高老师写出表格中的两个未知量a和b的值,并根据表格所给信息写出函数解析式(只需在答题卡的相应位置填写答案,无需写出解析过程);
(2)将![]() 图像上所有点向左平行移动
图像上所有点向左平行移动![]() 个单位长度,得到
个单位长度,得到![]() 图像,求
图像,求![]() 距离原点O最近的对称中心.
距离原点O最近的对称中心.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了12月1日至12月5日的每天昼夜温差与实验室每天每100颗种子中的发芽数,得到如下资料:
日期 | 12月1日 | 12月2日 | 12月3日 | 12月4日 | 12月5日 |
温差 | 10 | 11 | 13 | 12 | 8 |
发芽数 | 23 | 25 | 30 | 26 | 16 |
该农科所确定的研究方案是:先从这5组数据中选取2组,用剩下的3组数据求线性回归方程,再用被选取的2组数据进行检验.
(1)求选取的2组数据恰好是不相邻2天的数据的概率;
(2)若选取的是12月1日与12月5日的2组数据,请根据12月2日至4日的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,由线性回归方程得到的估计数据与所选取的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(2)中所得的线性回归方程是否可靠?
,由线性回归方程得到的估计数据与所选取的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(2)中所得的线性回归方程是否可靠?
附:参考公式: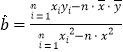 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从2名男生和2名女生中任意选择两人在星期六、星期日参加某公益活动,每天一人,则星期六安排一名男生、星期日安排一名女生的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com