
【题目】已知函数![]()
![]() 的部分图象如图所示.
的部分图象如图所示.

(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求函数![]() 在
在![]() 上的单调区间;
上的单调区间;
(Ⅲ)若对任意![]() 都有
都有![]() ,求实数m的取值范围.
,求实数m的取值范围.
【答案】(Ⅰ)![]() ,
,![]() ;(Ⅱ)单调递增区间为
;(Ⅱ)单调递增区间为![]() 和
和![]() ,单调递减区间为
,单调递减区间为![]() ;(Ⅲ)
;(Ⅲ)![]() ;
;
【解析】
(Ⅰ)根据三角函数的部分图象求出![]()
![]() 和
和![]() 的值;
的值;
(Ⅱ)由(Ⅰ)写出函数![]() 的解析式,再求函数在
的解析式,再求函数在![]() ,
,![]() 上的单调递增区间和单调递减区间;
上的单调递增区间和单调递减区间;
(Ⅲ)由(Ⅱ)求出函数![]() 在
在![]() ,
,![]() 的最大值和最小值,得出
的最大值和最小值,得出![]() 的最大值,从而求得
的最大值,从而求得![]() 的取值范围.
的取值范围.
(Ⅰ)设函数![]() 的最小正周期为
的最小正周期为![]() ,
,
由图可知,![]() ,所以
,所以![]() ,
,
又![]() ,
,![]() ,所以
,所以![]() ;
;
又![]() ,所以
,所以![]() ,
,
因为![]() ,所以
,所以![]() ,
,
所以![]() ,即
,即![]() ;
;
(Ⅱ)由(Ⅰ)知,![]() ,
,
因为当![]() 时,
时,![]() ,
,
所以当![]() ,即
,即![]() 时,
时,![]() 单调递增;
单调递增;
当![]() ,即
,即![]() 时,
时,![]() 单调递减;
单调递减;
当![]() ,即
,即![]() 时,
时,![]() 单调递增.
单调递增.
所以函数![]() 单调递增区间为
单调递增区间为![]() 和
和![]() ,单调递减区间为
,单调递减区间为![]() ;
;
(Ⅲ)由(Ⅱ)可知,函数![]() 在
在![]() 的最大值为
的最大值为![]() ,最小值为
,最小值为![]() ,
,
所以对任意![]() ,都有
,都有![]() ,
,
且当![]() ,
,![]() 时,
时,![]() 取到最大值
取到最大值![]() ,
,
又因为对任意![]() ,都有
,都有![]() 成立,
成立,
所以![]() ,即
,即![]() 的取值范围是
的取值范围是![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】节约资源和保护环境是中国的基本国策.某化工企业,积极响应国家要求,探索改良工艺,使排放的废气中含有的污染物数量逐渐减少.已知改良工艺前所排放的废气中含有的污染物数量为![]() ,首次改良后所排放的废气中含有的污染物数量为
,首次改良后所排放的废气中含有的污染物数量为![]() .设改良工艺前所排放的废气中含有的污染物数量为
.设改良工艺前所排放的废气中含有的污染物数量为![]() ,首次改良工艺后所排放的废气中含有的污染物数量为
,首次改良工艺后所排放的废气中含有的污染物数量为![]() ,则第n次改良后所排放的废气中的污染物数量
,则第n次改良后所排放的废气中的污染物数量![]() ,可由函数模型
,可由函数模型![]() 给出,其中n是指改良工艺的次数.
给出,其中n是指改良工艺的次数.
(1)试求改良后所排放的废气中含有的污染物数量的函数模型;
(2)依据国家环保要求,企业所排放的废气中含有的污染物数量不能超过![]() ,试问至少进行多少次改良工艺后才能使得该企业所排放的废气中含有的污染物数量达标.
,试问至少进行多少次改良工艺后才能使得该企业所排放的废气中含有的污染物数量达标.
(参考数据:取![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】襄阳市拟在2021年奥体中心落成后申办2026年湖北省省运会,据了解,目前武汉,宜昌,黄石等申办城市因市民担心赛事费用超支而准备相继退出,某机构为调查襄阳市市民对申办省运会的态度,选取某小区的100位居民调查结果统计如下:
支持 | 不支持 | 合计 | |
年龄不大于50岁 | 60 | ||
年龄大于50岁 | 10 | ||
合计 | 80 | 100 |
(1)根据已知数据,把表格数据填写完整;
(2)能否在犯错误的概率不超过![]() 的前提下认为不同年龄与支持申办省运会无关?
的前提下认为不同年龄与支持申办省运会无关?
附: ![]() ,
, ![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人做试验,从一个装有标号为1,2,3,4的小球的盒子中,无放回地取两个小球,每次取一个,先取的小球的标号为![]() ,后取的小球的标号为
,后取的小球的标号为![]() ,这样构成有序实数对
,这样构成有序实数对![]()
(1)写出这个试验的所有结果;
(2)求“第一次取出的小球上的标号为![]() ”的概率.
”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从高三抽出![]() 名学生参加数学竞赛,由成绩得到如下的频率分布直方图.试利用频率分布直方图求:
名学生参加数学竞赛,由成绩得到如下的频率分布直方图.试利用频率分布直方图求:
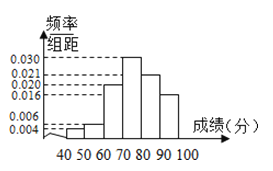
(1)这![]() 名学生成绩的众数与中位数;
名学生成绩的众数与中位数;
(2)这![]() 名学生的平均成绩.
名学生的平均成绩.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,函数
,函数![]() .
.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)若关于![]() 的方程
的方程![]() 的解集中恰有一个元素,求
的解集中恰有一个元素,求![]() 的取值范围;
的取值范围;
(3)设![]() ,若对任意
,若对任意![]() ,函数
,函数![]() 在区间
在区间![]() 上的最大值与最小值的差不超过1,求
上的最大值与最小值的差不超过1,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从分别写有1,2,3,4的4张卡片中随机抽取1张,放回后再随机抽取1张,则抽得的第一张卡片上的数大于第二张卡片上的数的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着我国互联网信息技术的发展,网络购物已经成为许多人消费的一种重要方式,某市为了了解本市市民的网络购物情况,特委托一家网络公示进行了网络问卷调查,并从参与调查的10000名网民中随机抽取了200人进行抽样分析,得到了下表所示数据:
经常进行网络购物 | 偶尔或从不进行网络购物 | 合计 | |
男性 | 50 | 50 | 100 |
女性 | 60 | 40 | 100 |
合计 | 110 | 90 | 200 |
(1)依据上述数据,能否在犯错误的概率不超过![]() 的前提下认为该市市民进行网络购物的情况与性别有关?
的前提下认为该市市民进行网络购物的情况与性别有关?
(2)现从所抽取的女性网民中利用分层抽样的方法再抽取![]() 人,从这
人,从这![]() 人中随机选出
人中随机选出![]() 人赠送网络优惠券,求出选出的
人赠送网络优惠券,求出选出的![]() 人中至少有两人是经常进行网络购物的概率;
人中至少有两人是经常进行网络购物的概率;
(3)将频率视为概率,从该市所有的参与调查的网民中随机抽取![]() 人赠送礼物,记经常进行网络购物的人数为
人赠送礼物,记经常进行网络购物的人数为![]() ,求
,求![]() 的期望和方差.
的期望和方差.
附:![]() ,其中
,其中![]()

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() 为自然对数的底数,
为自然对数的底数,![]() .
.
(1)讨论函数![]() 的单调性,并写出相应的单调区间;
的单调性,并写出相应的单调区间;
(2)已知![]() ,
,![]() ,若
,若![]() 对任意
对任意![]() 都成立,求
都成立,求![]() 的最大值;
的最大值;
(3)设![]() ,若存在
,若存在![]() ,使得
,使得![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com