
如图,已知圆中两条弦 与
与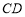 相交于点
相交于点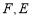 是
是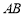 延长线上一点,且
延长线上一点,且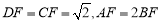 ,若
,若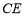 与圆相切,且
与圆相切,且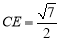 ,则
,则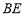 = .
= .

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2013-2014学年甘肃省武威市高三数学专题训练选择填空限时练一(解析版) 题型:选择题
已知椭圆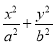 =1 (a>b>0),A(2,0)为长轴的一个端点,弦BC过椭圆的中心O,且
=1 (a>b>0),A(2,0)为长轴的一个端点,弦BC过椭圆的中心O,且 ·
· =0,|
=0,| -
- |=2|
|=2| -
- |,则其焦距为( )
|,则其焦距为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年甘肃省张掖市高三第三次诊断考试文科数学试卷(解析版) 题型:解答题
已知三棱柱ABC-A1B1C1中,侧棱垂直于底面,AC=BC,点D是AB的中点.

(1)求证:BC1∥平面CA1D;
(2)求证:平面CA1D⊥平面AA1B1B;
(3)若底面ABC为边长为2的正三角形,BB1= 求三棱锥B1-A1DC的体积.
求三棱锥B1-A1DC的体积.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖南省高三十三校联考第二次考试理科数学试卷(解析版) 题型:填空题
给定有限单调递增数列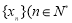 ,数列
,数列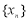 至少有两项)且
至少有两项)且
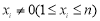 ,定义集合
,定义集合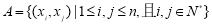 .若对任意点
.若对任意点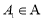 ,
,
存在点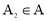 使得
使得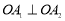
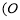 为坐标原点),则称数列
为坐标原点),则称数列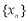 具有性质
具有性质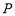 .
.
(1)给出下列四个命题,其中正确的是 .(填上所有正确命题的序号)
①数列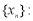 -2,2具有性质
-2,2具有性质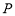 ;
;
②数列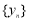 :-2,-1,1,3具有性质
:-2,-1,1,3具有性质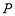 ;
;
③若数列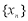 具有性质
具有性质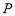 ,则
,则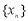 中一定存在两项
中一定存在两项 ,使得
,使得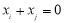 ;
;
④若数列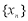 具有性质
具有性质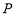 ,
,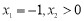 且
且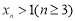 ,则
,则 .
.
(2)若数列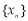 只有2014项且具有性质
只有2014项且具有性质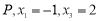 ,则
,则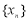 的所有项和
的所有项和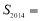 .
.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖南省高三十三校联考第二次考试理科数学试卷(解析版) 题型:选择题
如图,给定由10个点(任意相邻两点距离为1)组成的正三角形点阵,在其中任意取三个点,以这三个点为顶点构成的正三角形的个数是( )

A.12 B.13
C.15 D.16
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖南省高三十三校第二次联考文科数学试卷(解析版) 题型:填空题
P是椭圆上一定点,F1,F2是椭圆的两个焦点,若∠PF1 F2=60°,∠PF2F1=30°,则椭圆的离心率为 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖南省长沙市高考二模理科数学试卷(解析版) 题型:解答题
某联欢晚会举行抽奖活动,举办方设置了甲、乙两种抽奖方案,方案甲的中奖率为 ,中奖可以获得2分;方案乙的中奖率为
,中奖可以获得2分;方案乙的中奖率为 ,中奖可以获得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品.
,中奖可以获得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品.
(1)张三选择方案甲抽奖,李四选择方案乙抽奖,记他们的累计得分为X,若X≤3的概率为 ,求
,求 ;
;
(2)若张三、李四两人都选择方案甲或都选择方案乙进行抽奖,问:他们选择何种方案抽奖,累计得分的数学期望较大?
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖南省益阳市高三模拟考试理科数学试卷(解析版) 题型:解答题
已知椭圆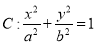 (
(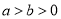 )的短轴长为2,离心率为
)的短轴长为2,离心率为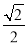 .过点M(2,0)的直线
.过点M(2,0)的直线 与椭圆
与椭圆 相交于
相交于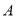 、
、 两点,
两点,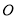 为坐标原点.
为坐标原点.
(1)求椭圆 的方程;
的方程;
(2)求 的取值范围;
的取值范围;
(3)若 点关于
点关于 轴的对称点是
轴的对称点是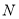 ,证明:直线
,证明:直线 恒过一定点.
恒过一定点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com