
某联欢晚会举行抽奖活动,举办方设置了甲、乙两种抽奖方案,方案甲的中奖率为 ,中奖可以获得2分;方案乙的中奖率为
,中奖可以获得2分;方案乙的中奖率为 ,中奖可以获得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品.
,中奖可以获得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品.
(1)张三选择方案甲抽奖,李四选择方案乙抽奖,记他们的累计得分为X,若X≤3的概率为 ,求
,求 ;
;
(2)若张三、李四两人都选择方案甲或都选择方案乙进行抽奖,问:他们选择何种方案抽奖,累计得分的数学期望较大?
(1)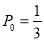 ;(2)详见解析.
;(2)详见解析.
【解析】
试题分析:(1)记“这2人的累计得分X≤3”的事件为A,依题意,两人累计得分的可能值为 ,故事件“
,故事件“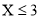 ”的对立事件为“
”的对立事件为“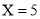 ”,所以所求事件的概率
”,所以所求事件的概率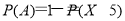 ;(2)因为每次抽奖中奖与否互不影响,且对方案甲或方案乙而言,中奖的概率不变,故对于张三、李四两人抽奖可看成两次独立重复试验,其中奖次数服从二项分布,设张三、李四都选择方案甲抽奖中奖次数为X1,都选择方案乙抽奖中奖次数为X2,则X1~
;(2)因为每次抽奖中奖与否互不影响,且对方案甲或方案乙而言,中奖的概率不变,故对于张三、李四两人抽奖可看成两次独立重复试验,其中奖次数服从二项分布,设张三、李四都选择方案甲抽奖中奖次数为X1,都选择方案乙抽奖中奖次数为X2,则X1~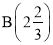 ,X2~B
,X2~B ,则累计得分的期望为E(2X1),E(3X2),从而比较大小即可.
,则累计得分的期望为E(2X1),E(3X2),从而比较大小即可.
(1)由已知得,张三中奖的概率为 ,李四中奖的概率为
,李四中奖的概率为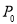 ,且两人中奖与否互不影响.
,且两人中奖与否互不影响.
记“这2人的累计得分X≤3”的事件为A,则事件A的对立事件为“X=5”,
因为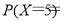
 ×
×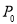 ,所以
,所以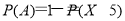 =1-
=1- ×
×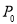 =
=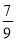 ,所以
,所以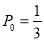 . 6分
. 6分
(2)设张三、李四都选择方案甲抽奖中奖次数为X1,都选择方案乙抽奖中奖次数为X2,
则这两人选择方案甲抽奖累计得分的数学期望为E(2X1),
选择方案乙抽奖累计得分的数学期望为E(3X2).
由已知可得,X1~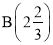 ,X2~B
,X2~B ,
,
所以E(X1)=2×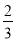 =
=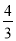 ,E(X2)=2×
,E(X2)=2×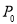 ,
,
从而E(2X1)=2E(X1)=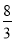 ,E(3X2)=3E(X2)=6
,E(3X2)=3E(X2)=6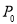 .
.
若 ,即
,即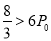 ,所以
,所以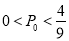 ;
;
若 ,即
,即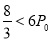 ,所以
,所以 ;
;
若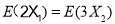 ,即
,即 ,所以
,所以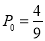 .
.
综上所述:当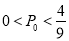 时,他们都选择方案甲进行抽奖时,累计得分的数学期望较大;当
时,他们都选择方案甲进行抽奖时,累计得分的数学期望较大;当 时,他们都选择方案乙进行抽奖时,累计得分的数学期望较大;当
时,他们都选择方案乙进行抽奖时,累计得分的数学期望较大;当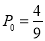 时,他们都选择方案甲或乙进行抽奖时,累计得分的数学期望相等. 12分
时,他们都选择方案甲或乙进行抽奖时,累计得分的数学期望相等. 12分
考点:1、对立事件;2、二项分布的期望.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2013-2014学年湖南省高三十三校联考第二次考试理科数学试卷(解析版) 题型:填空题
如图,已知圆中两条弦 与
与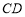 相交于点
相交于点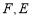 是
是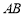 延长线上一点,且
延长线上一点,且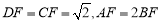 ,若
,若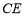 与圆相切,且
与圆相切,且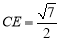 ,则
,则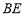 = .
= .

查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖南省高三十三校第二次联考文科数学试卷(解析版) 题型:选择题
在 中,若
中,若 分别为
分别为 的对边,且
的对边,且 ,则有( )
,则有( )
A.a、c、b成等比数列 B.a、c、b成等差数列
C.a、b、c成等差数列 D.a、b、c成等比数列
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖南省高三十三校第二次联考文科数学试卷(解析版) 题型:选择题
等差数列{ }的前规项和为Sn,S3=6,公差d=3,则a4=( )
}的前规项和为Sn,S3=6,公差d=3,则a4=( )
A.8 B.9 C.11 D.12
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖南省长沙市高考二模理科数学试卷(解析版) 题型:填空题
设点P是双曲线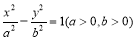 与圆x2+y2=a2+b2在第一象限的交点,其中F1,F2分别是双曲线的左、右焦点,且
与圆x2+y2=a2+b2在第一象限的交点,其中F1,F2分别是双曲线的左、右焦点,且 ,则双曲线的离心率为______.[来
,则双曲线的离心率为______.[来
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖南省长沙市高考二模理科数学试卷(解析版) 题型:选择题
设变量x,y满足约束条件 ,则z=x-3y的最大值为( )
,则z=x-3y的最大值为( )
A.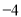 B.4 C.3 D.
B.4 C.3 D.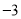
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com