
| A. | ②④ | B. | ②③ | C. | ③④ | D. | ①②③ |
分析 推导出命题p:?x∈R,使得sinx=$\frac{3}{2}$是假命题,命题q:?x∈R,都有x2-x+1=(x-$\frac{1}{2}$)2+$\frac{3}{4}$>0是真命题,由此利用复合命题的真假判断能求出结果.
解答 解:命题p:?x∈R,使得sinx=$\frac{3}{2}$是假命题,
命题q:?x∈R,都有x2-x+1=(x-$\frac{1}{2}$)2+$\frac{3}{4}$>0是真命题,
在①中,命题“p∧q”是假命题,故①错误;
在②中,命题“p∧(¬q)”是假命题,故②正确;
在③中,命题“(¬p)∧q”是真命题,故③正确;
在④中,命题“p∨q”是真命题,故④错误.
故选:B.
点评 本题考查考查命题真假的判断,考查复合命题真假判断、正弦函数、一元二次不等式等基础知识,考查推理论能力、运算求解能力,考查化归与转化思想、函数与方程思想,是基础题.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
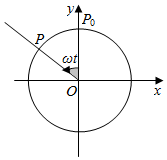 如图,点P是半径为1的砂轮边缘上的一个质点,它从初始位置P0开始,按逆时针方向以角速度ω=1rad/s做圆周运动,记点P的纵坐标y关于时间t(t≥0,t的单位:s)的函数关系为y=f(t).
如图,点P是半径为1的砂轮边缘上的一个质点,它从初始位置P0开始,按逆时针方向以角速度ω=1rad/s做圆周运动,记点P的纵坐标y关于时间t(t≥0,t的单位:s)的函数关系为y=f(t).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 对立事件 | B. | 不可能事件 | ||
| C. | 互斥但不对立事件 | D. | 以上都不对 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com