
【题目】设各项均为正数的数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,![]() (
(![]() ,
,![]() ),数列
),数列![]() 满足
满足![]() (
(![]() ).
).
(1)求数列![]() 、
、![]() 的通项公式;
的通项公式;
(2)设![]() ,
,![]() 是
是![]() 的前
的前![]() 项和,求正整数
项和,求正整数![]() ,使得对任意的
,使得对任意的![]() ,
,
均有![]() ;
;
(3)设![]() ,且
,且![]() ,其中
,其中![]() (
(![]() ,
,![]() ),求集合
),求集合![]() 中所有元素的和.
中所有元素的和.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)见解析.
;(3)见解析.
【解析】
(1)①a1=1,an2=Sn+Sn﹣1(n∈N*,n≥2),![]() Sn+1+Sn,相减可得:
Sn+1+Sn,相减可得:![]() an+1+an,化简利用已知条件及其等差数列的通项公式可得an.
an+1+an,化简利用已知条件及其等差数列的通项公式可得an.
②数列{bn}满足![]() (n∈N*).n≥2时,b1b2…bn﹣1
(n∈N*).n≥2时,b1b2…bn﹣1![]() ,相除可得bn.
,相除可得bn.
(2)cn![]() ,利用求和公式与裂项求和方法可得:Tn
,利用求和公式与裂项求和方法可得:Tn![]() .作差Tn+1﹣Tn,利用其单调性即可得出.
.作差Tn+1﹣Tn,利用其单调性即可得出.
(3)x=k1b1+k2b2+…+knbn,且x>0,其中k1,k2,…,kn∈{﹣1,1}(n∈N*,n≥2),
①要使x>0,则必须kn=1.其它k1,k2,…,kn﹣1∈{﹣1,1}(n∈N*,n≥2),可任取1,﹣1.通过放缩及其求和公式即可证明.另外kn=1.此时:x≥﹣2﹣22﹣……﹣2n﹣1+2n>0.
②其它k1,k2,…,kn﹣1∈{﹣1,1}(n∈N*,n≥2),可任取1,﹣1.此时集合内的元素x共有2n﹣1个互不相同的正数,利用乘法原理可得:表示x的式子共有2n﹣1个.利用反证法证明这2n﹣1个式子所表示的x互不相等,再分析求解所有元素的和.
(1)①a1=1,an2=Sn+Sn﹣1(n∈N*,n≥2),
∴![]() Sn+1+Sn,相减可得:
Sn+1+Sn,相减可得:![]() an+1+an,
an+1+an,
化为:(an+1+an)(an+1﹣an﹣1)=0,
∵an+1+an>0,
∴an+1﹣an=1,
又![]() S2+S1,可得
S2+S1,可得![]() a2﹣2=0,a2>0,
a2﹣2=0,a2>0,
解得:a2=2,
∴a2﹣a1=1,
∴数列{an}设等差数列,an=1+n﹣1=n.
②数列{bn}满足![]() (n∈N*).
(n∈N*).
n≥2时,b1b2…bn﹣1![]() ,
,
∴![]() .
.
(2)cn![]() ,
,
∴Tn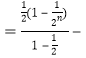 (1
(1![]() )
)![]() .
.
Tn+1﹣Tn![]() (
(![]() )
)![]() .
.
n≤3时,Tn+1≥Tn.
n≥4时,Tn+1≤Tn.
当m=4时,使得对任意的n∈N*,均有Tm≥Tn.
(3)x=k1b1+k2b2+…+knbn,且x>0,其中k1,k2,…,kn∈{﹣1,1}(n∈N*,n≥2),
①要使x>0,则必须kn=1.其它k1,k2,…,kn﹣1∈{﹣1,1}(n∈N*,n≥2),可任取1,﹣1.
证明:若kn=﹣1,则x=k12+k222+…+kn﹣12n﹣1﹣kn2n≤2+22+……+2n﹣1﹣2n![]() 2n=﹣2<0,
2n=﹣2<0,
此时x恒为负数,不成立.
∴kn=1.此时:x≥﹣2﹣22﹣……﹣2n![]() 2n=2>0,
2n=2>0,
故k1,k2,…,kn﹣1∈{﹣1,1}(n∈N*,n≥2),可任取1,﹣1.
②其它k1,k2,…,kn﹣1∈{﹣1,1}(n∈N*,n≥2),可任取1,﹣1.
此时集合内的元素x共有2n﹣1个互不相同的正数.
证明:k1,k2,…,kn﹣1∈{﹣1,1}(n∈N*,n≥2),
利用乘法原理可得:表示x的式子共有2n﹣1个.
下面证明这2n﹣1个式子所表示的x互不相等,具体如下:
证明:假如这2n﹣1个式子所表示的x存在相等的数,
x1=2n+kn﹣12n﹣1+……+k222+k12=x2=2n![]() 2n﹣1
2n﹣1![]() 22
22![]() 2.ki,
2.ki,![]() ∈{﹣1,1}(i∈N*,n﹣1≥i≥2),
∈{﹣1,1}(i∈N*,n﹣1≥i≥2),
即满足ki![]() ∈{﹣1,1}(i∈N*,n﹣1≥i≥2)的第一组系数的下标数为m.
∈{﹣1,1}(i∈N*,n﹣1≥i≥2)的第一组系数的下标数为m.
则![]() 2m
2m![]() 2m﹣1+(
2m﹣1+(![]() )2m﹣2+……+(
)2m﹣2+……+(![]() )2,
)2,
而|![]() 2m﹣1+(
2m﹣1+(![]() )2m﹣2+……+(
)2m﹣2+……+(![]() )2|≤22m﹣1+22m﹣2+……+2×2=2m+1﹣4<|
)2|≤22m﹣1+22m﹣2+……+2×2=2m+1﹣4<|![]() 2m|<2m+1.
2m|<2m+1.
因此,假设不成立,即这2n﹣1个式子所表示的x
③这2n﹣1个x互不相等的正数x(每个均含knbn=2n).
又ki=1或﹣1(i=1,2,……,n﹣1)等可能出现,因此所有kibi(i=1,2,……,n﹣1)部分的和为0.
故集合B中所有元素的和为所有knbn=2n的和,即2n2n﹣1=22n﹣1.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的一个焦点为
的一个焦点为![]() ,点
,点![]() 在
在![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() :
:![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,问
两点,问![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 是以
是以![]() 为直角顶点的等腰直角三角形?若存在,求点
为直角顶点的等腰直角三角形?若存在,求点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为研究男、女生的身高差异,现随机从高二某班选出男生、女生各10人,并测量他们的身高,测量结果如下(单位:厘米):
男:164 178 174 185 170 158 163 165 161 170
女:165 168 156 170 163 162 158 153 169 172
(1)根据测量结果完成身高的茎叶图(单位:厘米),并分别求出男、女生身高的平均值.

(2)请根据测量结果得到20名学生身高的中位数![]() (单位:厘米),将男、女生身高不低于
(单位:厘米),将男、女生身高不低于![]() 和低于
和低于![]() 的人数填入下表中,并判断是否有
的人数填入下表中,并判断是否有![]() 的把握认为男、女生身高有差异?
的把握认为男、女生身高有差异?
人数 | 男生 | 女生 |
身高 | ||
身高 |
参照公式:![]()
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | .024 | 6.635 | 7.879 | 10.828 |
(3)若男生身高低于165厘米为偏矮,不低于165厘米且低于175厘米为正常,不低于175厘米为偏高.假设可以用测量结果的频率代替概率,试求从高二的男生中任意选出2人,恰有1人身高属于正常的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,其上一点
,其上一点![]() 在准线上的射影为
在准线上的射影为![]() ,△
,△![]() 恰为一个边长为4的等边三角形.
恰为一个边长为4的等边三角形.
(1)求抛物线![]() 的方程;
的方程;
(2)若过定点![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于
于![]() ,
,![]() 两点,
两点,![]() 为坐标原点)的面积为
为坐标原点)的面积为![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分16分)
在平面直角坐标系xOy中,椭圆C:![]() (a>b>0)的上顶点到焦点的距离为2,离心率为
(a>b>0)的上顶点到焦点的距离为2,离心率为![]() .
.
(1)求a,b的值.
(2)设P是椭圆C长轴上的一个动点,过点P作斜率为k的直线l交椭圆C于A、B两点.
(ⅰ)若k=1,求△OAB面积的最大值;
(ⅱ)若PA2+PB2的值与点P的位置无关,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() ,直线
,直线 ![]() .以极点
.以极点![]() 为原点,极轴为
为原点,极轴为![]() 轴的正半轴建立平面直角坐标系.
轴的正半轴建立平面直角坐标系.
(1)求直线![]() ,
,![]() 的直角坐标方程以及曲线
的直角坐标方程以及曲线![]() 的参数方程;
的参数方程;
(2)已知直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,直线
两点,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列有关命题的说法正确的是__________________.
①命题“若x2-3x+2=0,则x=1”的逆否命题为:若x≠1,则x2-3x+2≠0
②x=1是x2-3x+2=0的充分不必要条件
③若p∧q为假命题,则p,q均为假命题
④对于命题p:x∈R,使得x2+x+1<0,则非p:x∈R, 均有x2+x+1≥0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列有关平面向量分解定理的四个命题:
(1)一个平面内有且只有一对不平行的向量可作为表示该平面所有向量的基;
(2)一个平面内有无数多对不平行向量可作为表示该平面内所有向量的基;
(3)平面向量的基向量可能互相垂直;
(4)一个平面内任一非零向量都可唯一地表示成该平面内三个互不平行向量的线性组合.
其中正确命题的个数是( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com