
| A. | $\frac{3}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{5}{4}$ |
分析 根据对数函数的性质得出定点坐标,运用诱导公式化简求值.
解答 解:∵函数f(x)=loga(x-3)+5(a>0且a≠1)的图象过定点P,
∴定点P(4,5),
∴tanα=$\frac{5}{4}$,
∵$\frac{cos(\frac{11π}{2}-α)sin(\frac{9π}{2}+α)}{cos(\frac{π}{2}+α)sin(-π-α)}$=$\frac{cos(6π-\frac{π}{2}-α)}{cos(\frac{π}{2}+α)}$•$\frac{sin(4π+\frac{π}{2}+α)}{sin(-2π+π-α)}$=$\frac{cos(\frac{π}{2}+α)}{cos(\frac{π}{2}+α)}$$•\frac{cosα}{sinα}$=$\frac{1}{tanα}$=$\frac{4}{5}$,
∴$\frac{cos(\frac{11π}{2}-α)sin(\frac{9π}{2}+α)}{cos(\frac{π}{2}+α)sin(-π-α)}$=$\frac{4}{5}$,
故选:C.
点评 本题考查了三角函数的定义,诱导公式的运用求值,准确灵活应用公式,是解题的关键.


科目:高中数学 来源: 题型:选择题
| A. | $[{2,\frac{5}{2}}]$ | B. | $[{\frac{5}{4},\frac{5}{2}}]$ | C. | $[{\frac{4}{5},\frac{5}{2}}]$ | D. | $[{\frac{5}{4},2}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
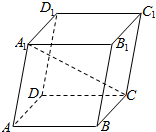 如图所示的平行六面体ABCD-A1B1C1D中,AB=AD=AA1=1,∠BAD=90°,∠BAA1=∠DAA1=60°,则CA1的长=1.
如图所示的平行六面体ABCD-A1B1C1D中,AB=AD=AA1=1,∠BAD=90°,∠BAA1=∠DAA1=60°,则CA1的长=1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
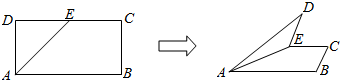
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{2}-{y^2}=1$ | B. | ${y^2}-\frac{x^2}{2}=1$ | C. | ${x^2}-{\frac{y}{2}^2}=1$ | D. | $\frac{y^2}{2}-{x^2}=1$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com