练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    在等差数列{an}中，已知公差d＝2，a2是a1与a4的等比中项．

    (1)求数列{an}的通项公式；

    (2)设bn＝，记Tn＝－b1＋b2－b3＋b4－…＋(－1)nbn，求Tn.


    解　(1)由题意知(a1＋d)2＝a1(a1＋3d)，

    即(a1＋2)2＝a1(a1＋6)，解得a1＝2，

    所以数列{an}的通项公式为an＝2n.

    (2)由题意知bn＝＝n(n＋1)，

    所以Tn＝－1×2＋2×3－3×4＋…＋(－1)nn·(n＋1)．

    因为bn＋1－bn＝2(n＋1)，可得当n为偶数时，

    Tn＝(－b1＋b2)＋(－b3＋b4)＋…＋(－bn－1＋bn)


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    如图，△ABC中，∠ACB=90°，AC=BC，AE是BC边上的中线，过C作CF⊥AE，垂足为F，过B作BD⊥BC交CF的延长线于D．

    （1）求证：AE=CD；

    （2）若AC=12cm，求BD的长．

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，在等腰直角三角形ABC中，斜边BC＝2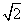，过点A作BC的垂线，垂足为A1；过点A1作AC的垂线，垂足为A2；过点A2作A1C的垂线，垂足为A3；…，依此类推，设BA＝a1，AA1＝a2，A1A2＝a3，…，A5A6＝a7，则a7＝________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知{an}是等差数列，公差为d，首项a1＝3，前n项和为Sn.令cn＝(－1)nSn(n∈N*)，{cn}的前20项和T20＝330.数列{bn}满足bn＝2(a－2)dn－2＋2n－1，a∈R.

    (1)求数列{an}的通项公式；

    (2)若bn＋1≤bn，n∈N*，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知数列{an}的通项公式为an＝n2cosnπ(n∈N*)，Sn为它的前n项和，则等于(　　)

    A．1 005                                B．1 006

    C．2 011                                D．2 012

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知数列{an}的前n项和为Sn满足：Sn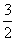＝an＋n－3.

    (1)求证：数列{an－1}是等比数列．

    (2)令cn＝log3(a1－1)＋log3(a2－1)＋…＋log3(an－1)，对任意n∈N*，是否存在正整数m，使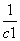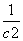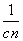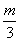＋＋…＋≥都成立？若存在，求出m的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设a＝＋2，b＝2＋，则a，b的大小关系为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    平面中的三角形和空间中的四面体有很多相类似的性质，例如在三角形中，(1)三角形两边之和大于第三边；(2)三角形的面积S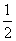＝×底×高；(3)三角形的中位线平行于第三边且等于第三边的；…

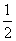    请类比上述性质，写出空间中四面体的相关结论．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝－x2＋ax＋b2－b＋1(a∈R，b∈R)，对任意实数x都有f(1－x)＝f(1＋x)成立，当x∈[－1,1]时，f(x)>0恒成立，则b的取值范围是(　　)

    A．－1<b<0                              B．b>2

    C．b<－1或b>2                          D．不能确定

    查看答案和解析>>

    同步练习册答案