
| A. | 一条 | B. | 两条 | C. | 三条 | D. | 四条 |
分析 当过点(0,2)的直线的斜率不存在时,直线的方程为x=0;当过点(0,2)的直线的斜率等于0时,直线的方程为y=2;当过点(0,2)的直线斜率存在且不为零时,设为k,把y=kx+2,代入抛物线方程,由判别式等于0,求得k的值,从而得到结论.
解答 解:抛物线y2=8x的焦点为(2,0),
当过点(0,2)的直线的斜率不存在时,直线的方程为x=0,即直线为y轴时,与抛物线y2=8x只有一个公共点.
当过点(0,2)的直线的斜率等于0时,直线的方程为y=2,与抛物线y2=8x只有一个公共点.
当过点(0,2)的直线斜率存在且不为零时,设为k,那么直线方程为:y+2=kx,即:y=kx+2,
代入抛物线方程,可得 k2x2+(4k-8)x+4=0,由判别式等于0 可得:64-64k=0,
∴k=1,此时,直线的方程为y=x+2.
综上,满足条件的直线共有3条,
故选:C.
点评 本题考查直线和圆锥曲线的位置关系,体现了分类讨论的数学思想,求出直线的斜率,是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
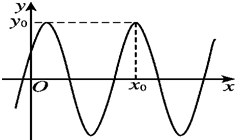 函数f(x)=2sin($\frac{2π}{3}$x+$\frac{π}{6}$)的部分图象如图所示.
函数f(x)=2sin($\frac{2π}{3}$x+$\frac{π}{6}$)的部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3π}{4}$ | B. | -$\frac{7π}{4}$ | C. | -$\frac{5π}{4}$ | D. | -$\frac{3π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
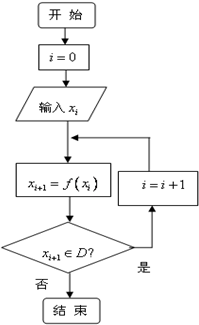 对任意函数f(x),x∈D,可按如图构造一个数列发生器,数列发生器产生数列{xn}.
对任意函数f(x),x∈D,可按如图构造一个数列发生器,数列发生器产生数列{xn}.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com