
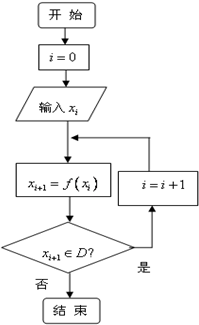
 对任意函数f(x),x∈D,可按如图构造一个数列发生器,数列发生器产生数列{xn}.
对任意函数f(x),x∈D,可按如图构造一个数列发生器,数列发生器产生数列{xn}.分析 (1)函数f(x)=$\frac{4x-2}{x+1}$的定义域D=(-∞,-1)∪(-1,+∞),由此能推导出数列{xn}只有三项x1=$\frac{11}{19}$,x2=$\frac{1}{5}$,x3=-1.
(2)f(x)=2x+3的定义域为R,若x0=-1,则x1=1,则xn+1+3=2(xn+3),从而得到数列{xn+3}是首项为4,公比为2的等比数列,由此能求出数列{xn}的通项公式.
解答 解:(1)函数f(x)=$\frac{4x-2}{x+1}$的定义域D=(-∞,-1)∪(-1,+∞),…(1分)
把x0=$\frac{49}{65}$代入可得x1=$\frac{11}{19}$,把x1=$\frac{11}{19}$代入可得x2=$\frac{1}{5}$,把x2=$\frac{1}{5}$代入可得x3=-1,
因为x3=-1∉D,
所以数列{xn}只有三项:x1=$\frac{11}{19}$,x2=$\frac{1}{5}$,x3=-1.…(4分)
(2)f(x)=2x+3的定义域为R,…(6分)
若x0=-1,则x1=1,
则xn+1=f(xn)=2xn+3,
所以xn+1+3=2(xn+3),…(8分)
所以数列{xn+3}是首项为4,公比为2的等比数列,
所以xn+3=4•2n-1=2n+1,
所以xn=2n+1-3,
即数列{xn}的通项公式xn=2n+1-3. …(10分)
点评 本题考查数列的所有项的求法,考查数列的通项公式的求法,解题时要认真审题,仔细解答,注意等价转化思想的合理运用,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{5}}}{5}$ | B. | $-\frac{{\sqrt{5}}}{5}$ | C. | $\frac{{2\sqrt{5}}}{5}$ | D. | $-\frac{{2\sqrt{5}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 21 | B. | 22 | C. | 23 | D. | 24 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com