
分析 (1)求出函数f(x)在x=0处的导数和f(0)的值,结合直线方程的点斜式方程,可求切线方程;
(2)f(x)在x=x0处取得最小值必是函数的极小值,可以先通过讨论导数的零点存在性,得出函数有极小值的a的大致取值范围,然后通过极小值对应的x0∈(1,3),解关于a的不等式,从而得出取值范围.
解答 解:(1)f′(x)=3x2+6ax+3-6a,
由f(0)=12a-3,f′(0)=3-6a,
可得曲线y=f(x)在x=0处的切线方程为y=(3-6a)x+12a-3,
当x=2时,y=2(3-6a)+12a-3=3,可得点(2,3)在切线上,
∴曲线y=f(x)在x=0的切线过点(2,3);
(2)由f′(x)=0得,
x2+2ax+1-2a=0…(1)
方程(1)的根的判别式
△=4a2-4(1-2a)=4(a+1+$\sqrt{2}$) (a+1-$\sqrt{2}$)
①当-$\sqrt{2}$-1≤a≤$\sqrt{2}$-1时,函数f(x)没有极小值,
②当a<-$\sqrt{2}$-1或a>$\sqrt{2}$-1时,
由f′(x)=0得x1=-a-$\sqrt{{a}^{2}+2a-1}$,x2=-a+$\sqrt{{a}^{2}+2a-1}$,
故x0=x2,由题设可知1<-a+$\sqrt{{a}^{2}+2a-1}$<3
(i)当a>$\sqrt{2}$-1时,不等式1<-a+$\sqrt{{a}^{2}+2a-1}$<3没有实数解;
(ii)当a<-$\sqrt{2}$-1时,不等式1<-a+$\sqrt{{a}^{2}+2a-1}$<3
化为a+1<$\sqrt{{a}^{2}+2a-1}$<a+3,
解得-$\frac{5}{2}$<a<-$\sqrt{2}$-1,
综合①②,得a的取值范围是(-$\frac{5}{2}$,-$\sqrt{2}$-1).
点评 将字母a看成常数,讨论关于x的三次多项式函数的极值点,是解决本题的难点,本题中处理关于a的无理不等式,计算也比较繁,因此本题对能力的要求比较高.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1)(2) | B. | (1)(3) | C. | (1)(2)(4) | D. | (2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3π}{4}$ | B. | -$\frac{7π}{4}$ | C. | -$\frac{5π}{4}$ | D. | -$\frac{3π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
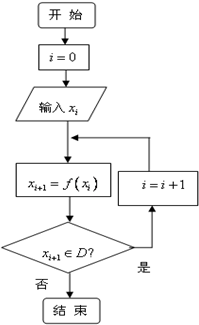 对任意函数f(x),x∈D,可按如图构造一个数列发生器,数列发生器产生数列{xn}.
对任意函数f(x),x∈D,可按如图构造一个数列发生器,数列发生器产生数列{xn}.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 等边三角形 | B. | 等腰直角三角形 | C. | 直角三角形 | D. | 等腰三角形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com