
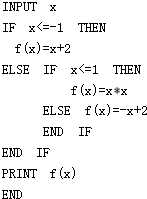
分析 分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是计算分段函数f(x)=$\left\{\begin{array}{l}{\stackrel{x+2}{{x}^{2}}}&{\stackrel{x≤-1}{-1<x≤1}}\\{-x+6}&{x>1}\end{array}\right.$的函数值;函数g(x)=f(x)-m在R上有且只有两个零点,则我们可以在同一平面直角坐标系中画出y=f(x)与y=m的图象进行分析,从而得解.
解答 解:分析程序中各变量、各语句的作用,
再根据流程图所示的顺序,可知:
该程序的作用是计算分段函数f(x)=$\left\{\begin{array}{l}{\stackrel{x+2}{{x}^{2}}}&{\stackrel{x≤-1}{-1<x≤1}}\\{-x+6}&{x>1}\end{array}\right.$的函数值;
其函数图象如图所示: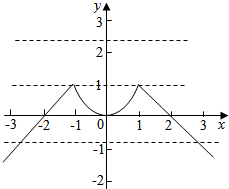
又∵函数g(x)=f(x)-m在R上有且只有两个零点,
则由图可得m<0或m=1,
故答案为:(-∞,0)∪{1}.
点评 本题考查程序框图以及函数的零点,通过对程序框图的理解,转化为函数图象,然后把函数零点转化为交点个数问题,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
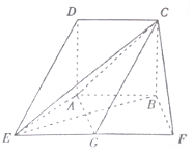 已知正方形ABCD的边长为4,且AB=AE=BF=$\frac{1}{2}$EF,AB∥EF,AD⊥底面AEFB,G是EF的中点.
已知正方形ABCD的边长为4,且AB=AE=BF=$\frac{1}{2}$EF,AB∥EF,AD⊥底面AEFB,G是EF的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
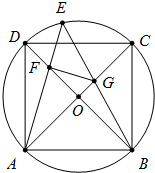 如图,ABCD是圆O的内接正方形,E是劣弧CD上一点,EA交BD于F,EB交AC于G,且GF⊥AE.
如图,ABCD是圆O的内接正方形,E是劣弧CD上一点,EA交BD于F,EB交AC于G,且GF⊥AE.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (-∞,1) | C. | (0,+∞) | D. | $(0,\frac{1}{2})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
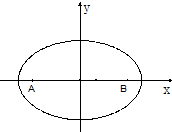 椭圆满足这样的光学性质:从椭圆的一个焦点发射的光线,经椭圆反射后,反射光线经过椭圆的另一个焦点.现有一个水平放置的椭圆形台球盘,满足方程$\frac{x^2}{64}+\frac{y^2}{28}=1$,点A,B是它的两个焦点.当静止的小球从点A开始出发,沿直线运动,经椭圆壁反射后再回到点A时,此时小球经过的路程可能是( )
椭圆满足这样的光学性质:从椭圆的一个焦点发射的光线,经椭圆反射后,反射光线经过椭圆的另一个焦点.现有一个水平放置的椭圆形台球盘,满足方程$\frac{x^2}{64}+\frac{y^2}{28}=1$,点A,B是它的两个焦点.当静止的小球从点A开始出发,沿直线运动,经椭圆壁反射后再回到点A时,此时小球经过的路程可能是( )| A. | 32或4或$16-4\sqrt{7}$ | B. | $16+4\sqrt{7}$或28或$16-4\sqrt{7}$ | ||
| C. | 28或4或$16+4\sqrt{7}$ | D. | 32或28或4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com