
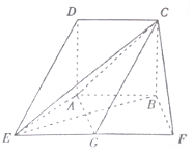
 已知正方形ABCD的边长为4,且AB=AE=BF=$\frac{1}{2}$EF,AB∥EF,AD⊥底面AEFB,G是EF的中点.
已知正方形ABCD的边长为4,且AB=AE=BF=$\frac{1}{2}$EF,AB∥EF,AD⊥底面AEFB,G是EF的中点.分析 (1)欲证明DE∥平面AGC,只需推知DE∥GC即可,根据已知条件可以判定四边形DEGC是平行四边形,则易证得DE∥GC;
(2)根据已知条件推知BC⊥AG;由正方形的性质和菱形的判定定理推知四边形AEGB是菱形,则该菱形的对角线相互垂直:AG⊥EB,易证得结论.
解答  (1)证明:在正方形ABCD中,CD=AB,CD∥AB.
(1)证明:在正方形ABCD中,CD=AB,CD∥AB.
∵AB∥EF,
∴CD∥EF,
∴CD∥EG.
又∵AB=$\frac{1}{2}$EF且G是EF的中点,
∴CD=GE,
∴四边形DEGC是平行四边形,
∴DE∥GC.
又∵ED?平面AGC,GC?平面AGC,
∴DE∥平面AGC
(2)证明:在正方形ABCD中,AD∥BC.
∵AD⊥底面AEFB,
∴BC⊥底面AEFB,
∴AG⊥BC.
又∵AB∥EF,AB=$\frac{1}{2}$EF且G是EF的中点,
∴AB=EG,
∴四边形AEGB是平行四边形,
又∵AB=AE,
∴平行四边形AEGB是菱形,
∴AG⊥EB.
又∵AG?平面BCE,BE∩BC=B,
∴AG⊥平面BCE.
点评 本题考查了直线与平面平行的判定,直线与平面垂直的判定.熟记判定定理即可证得结论,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
| 日需求量n(瓶) | 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 频数 | 5 | 5 | 8 | 12 | 10 | 6 | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | $2\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 有95%的把握认为两者有关 | |
| B. | 约有95%的心脏病患者使用药物有作用 | |
| C. | 有99%的把握认为两者有关 | |
| D. | 约有99%的心脏病患者使用药物有作用 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1)(2) | B. | (1)(3) | C. | (1)(2)(4) | D. | (2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com