
分析 (1)①当k不存在时,利用|MN|=|AB|=4判断;②当k存在时,设直线l:y=kx+4,通过直线与圆的位置关系求出直线的斜率,然后求解直线l方程.
(2)根据圆的对称性,猜想点C落在定直线y=1上,联立直线与圆的方程,利用韦达定理以及判别式,求出BM的方程,然后判断直线AN与BM的交点在一条定直线上.
解答 (1)解:①当k不存在时,|MN|=|AB|=4不符合题意
②当k存在时,设直线l:y=kx+4∵$|MN|=2\sqrt{3}$∴圆心O到直线l的距离$d=\sqrt{{2^2}-3}=1$,
∴$\frac{|4|}{{\sqrt{1+{k^2}}}}=1$,解得$k=±\sqrt{15}$
综上所述,满足题意的直线l方程为$y=±\sqrt{15}x+4$
(2)证明:设直线MN的方程为:y=kx+4,N(x1,y1)、M(x2,y2)
联立$\left\{\begin{array}{l}y=kx+4\\{x^2}+{y^2}=4\end{array}\right.$得:(1+k2)x2+8kx+12=0
∴$\left\{\begin{array}{l}△={(8k)^2}-48(1+{k^2})>0\\{x_1}+{x_2}=\frac{-8k}{{1+{k^2}}}\\{x_1}{x_2}=\frac{12}{{1+{k^2}}}\end{array}\right.$
直线AN:$\frac{y-2}{x}=\frac{{{y_1}-2}}{x_1}$,直线BM:$\frac{y+2}{x}=\frac{{{y_2}+2}}{x_2}$
消去x得:$\frac{y-2}{y+2}=\frac{{({y_1}-2){x_2}}}{{({y_2}+2){x_1}}}$
要证:C落在定直线y=1上,只需证:$\frac{1-2}{1+2}=\frac{{({y_1}-2){x_2}}}{{({y_2}+2){x_1}}}$
即证:$\frac{-1}{3}=\frac{{(k{x_1}+2){x_2}}}{{(k{x_2}+6){x_1}}}$
即证:-kx1x2-6x1=3kx1x2+6x2
即证:4kx1x2+6(x1+x2)=0
即证:$4k\frac{12}{{1+{k^2}}}-6\frac{8k}{{1+{k^2}}}=0$
显然成立.
所以直线AN与BM的交点在一条定直线上.
点评 本题考查直线、圆、用几何法与代数法研究直线与圆位置关系等基础知识,考查运算求解能力、推理论证能力,探究论证的能力,考查数形结合、分类与整合,化归与转化等数学思想.


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源: 题型:解答题
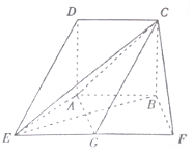 已知正方形ABCD的边长为4,且AB=AE=BF=$\frac{1}{2}$EF,AB∥EF,AD⊥底面AEFB,G是EF的中点.
已知正方形ABCD的边长为4,且AB=AE=BF=$\frac{1}{2}$EF,AB∥EF,AD⊥底面AEFB,G是EF的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (-∞,1) | C. | (0,+∞) | D. | $(0,\frac{1}{2})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 椭圆满足这样的光学性质:从椭圆的一个焦点发射的光线,经椭圆反射后,反射光线经过椭圆的另一个焦点.现有一个水平放置的椭圆形台球盘,满足方程$\frac{x^2}{64}+\frac{y^2}{28}=1$,点A,B是它的两个焦点.当静止的小球从点A开始出发,沿直线运动,经椭圆壁反射后再回到点A时,此时小球经过的路程可能是( )
椭圆满足这样的光学性质:从椭圆的一个焦点发射的光线,经椭圆反射后,反射光线经过椭圆的另一个焦点.现有一个水平放置的椭圆形台球盘,满足方程$\frac{x^2}{64}+\frac{y^2}{28}=1$,点A,B是它的两个焦点.当静止的小球从点A开始出发,沿直线运动,经椭圆壁反射后再回到点A时,此时小球经过的路程可能是( )| A. | 32或4或$16-4\sqrt{7}$ | B. | $16+4\sqrt{7}$或28或$16-4\sqrt{7}$ | ||
| C. | 28或4或$16+4\sqrt{7}$ | D. | 32或28或4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com