
| 日需求量n(瓶) | 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 频数 | 5 | 5 | 8 | 12 | 10 | 6 | 4 |
分析 (1)利用分段函数直接列出函数的解析式即可.
(2)随机变量X可取42,48,54,60,求出概率,列出分布列,然后求解期望即可.
解答 解:(Ⅰ)当日需求量n≥20时,利润y=60(元);
当日需求量n<20时,利润y=8n+2(20-n)-100=6n-60(元),
则利润y关于当天需求量n的函数解析式为:$y=\left\{\begin{array}{l}6n-60,n<20\\ 60,n≥20\end{array}\right.$(n∈N).…6分
(Ⅱ)随机变量X可取42,48,54,60,
则P(X=42)=0.1,P(X=48)=0.1,P(X=54)=0.16,P(X=60)=0.64,
随机变量X的分布列为
| X | 42 | 48 | 54 | 60 |
| P | 0.1 | 0.1 | 0.16 | 0.64 |
点评 本题考查分段函数的应用,离散型随机变量的分布列以及期望的求法,考查计算能力.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 4+20π | B. | 16+12π | C. | 16+16π | D. | 16+20π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
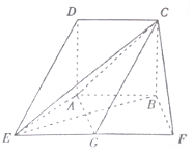 已知正方形ABCD的边长为4,且AB=AE=BF=$\frac{1}{2}$EF,AB∥EF,AD⊥底面AEFB,G是EF的中点.
已知正方形ABCD的边长为4,且AB=AE=BF=$\frac{1}{2}$EF,AB∥EF,AD⊥底面AEFB,G是EF的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com