
| A�� | ��1����2�� | B�� | ��1����3�� | C�� | ��1����2����4�� | D�� | ��2�� |
���� ���ж������Dz��Ǻ���������������������Ҫ���Dz��Ƿ��Ϻ������������������Ķ��壬�ж�һ�����������Ƿ�����������ؼ��ǿ����Ƿ������������Ķ��壬���Ƿ���������������Ƶ���һ��������������̣�����������ǿ��Ƿ������������Ķ��壮
��� �⣺��1��Ϊ���������������������Բ��������ȳ�����й����ʣ�
��2��Ϊ�������������Ϲ��������Ķ��壬���������һ����������̣�
��3������������
��4��Ϊ�������������Ϲ��������Ķ��壬���������һ����������̣�
��ѡ��C��
���� �ж�һ�����������Ƿ��ǹ��������ؼ��ǿ����Ƿ���Ϲ��������Ķ��壬���Ƿ��������һ����������̣�
�ж�һ�����������Ƿ�����������ؼ��ǿ����Ƿ������������Ķ��壬���Ƿ���������������Ƶ���һ��������������̣�
�ж�һ�����������Ƿ������������ؼ��ǿ����Ƿ�������������Ķ��壬�ܷ�������������ҳ��������ۡ���������ɲ��֣�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
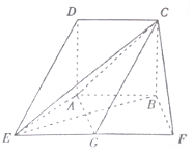 ��֪������ABCD�ı߳�Ϊ4����AB=AE=BF=$\frac{1}{2}$EF��AB��EF��AD�͵���AEFB��G��EF���е㣮
��֪������ABCD�ı߳�Ϊ4����AB=AE=BF=$\frac{1}{2}$EF��AB��EF��AD�͵���AEFB��G��EF���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y2=x | B�� | x2=-8y | C�� | y2=-x��x2=8y | D�� | y2=x��x2=-8y |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{{\sqrt{5}}}{5}$ | B�� | $-\frac{{\sqrt{5}}}{5}$ | C�� | $\frac{{2\sqrt{5}}}{5}$ | D�� | $-\frac{{2\sqrt{5}}}{5}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com